算法总结-数组&链表
算法总结-数组&链表
今天来说一说最简单的数据结构，数组和链表。
- 数组是逻辑和物理都连续的存储结构，可以说是存储数据最基本的数据结构。
- 链表逻辑顺序是通过指针依次链接起来的，物理上并不一定连续，有单链表，双向链表等。
概念什么的比较简单，基本应用也很简单。这么简单还为啥要单独写一篇呢？因为有些题目考察数组和链表花式操作，这种题目主要考察对简单的数据结构的理解，题目并不难，但每次写起来不是数组下标搞错了，就是链表断链了，每次都不能一次撸对代码，还要动手debug，所以干脆总结一下。不过既然动手总结了，把一些经典的题目也一起总结一下。
一维数组
一维数组有个相当经典的题目。LeetCode 189. 对数组循环右移k位，一个例子如下
before = [1, 2, 3, 4, 5, 6, 7]
k = 3
after = [5, 6, 7, 1, 2, 3, 4]
要求是in-place，也就是用O(1)的空间，这个题目做过无数遍了（所以直接跳过一步一步移动的愚蠢方法）。使用两次翻转的方法。具体如下：
[1, 2, 3, 4, 5, 6, 7] # 原始数组
[4, 3, 2, 1, 7, 6, 5] # 第一次：分别reverse前n-k个与后k个
[5, 6, 7, 1, 2, 3, 4] # 第二次：reverse整个数组。
代码也很简单（C++代码如下）。python可以用切片做，一行就写完了，就不贴代码了。
class Solution_189 {
public:
void _rotate(vector<int> &nums, int left, int right){
while (left < right){
int t = nums[left];
nums[left] = nums[right];
nums[right] = t;
left ++;
right --;
}
}
void rotate(vector<int>& nums, int k) {
int n = nums.size();
k = k % n;
_rotate(nums, n-k, n-1);
_rotate(nums, 0, n-k-1);
_rotate(nums, 0, n-1);
}
};
链表也有类似的题目，但不同的是，链表移动数据不需要一个一个拷贝，只需要从链上取下在插入就好了，对于这个题目的具体做法在下面单链表部分。
二维数组
LeetCode 48. 顺时针旋转一个二维n阶矩阵90°，这在图像操作中经常用到，要求in-place（注意必须是n阶矩阵才能in-place，否则旋转之后shape不一致）。使用额外的空间来旋转的话就太简单了。考虑一个简单的例子:
# 原二维数组
[
[1,2,3],
[4,5,6],
[7,8,9]
]
其顺时针旋转90°的结果为:
# 顺时针旋转90°结果
[
[7,4,1],
[8,5,2],
[9,6,3]
]
这题的关键在于矩阵转置，上述原始矩阵转置的结果为
# 转置的结果
[
[1,4,7],
[2,5,8],
[3,6,9]
]
对比转置和旋转的结果，发现顺时针旋转就是将转置后再对每一行reverse。
class Solution_48:
def rotate(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
n = len(matrix)
for i in range(n):
for j in range(i):
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
for i in range(n):
lo, hi = 0, n - 1
while lo < hi:
matrix[i][lo], matrix[i][hi] = matrix[i][hi], matrix[i][lo]
lo += 1
hi -= 1
还可以联想发现，逆时针旋转90°只需要转置后再对每一列reverse就好了。而旋转180°只需要横着对每一行reverse一遍，然后竖着对每一列revese一遍（举一反三）。
LeetCode 54.给定一个m x n矩阵，以螺旋顺序输出其中的矩阵的元素。例如
# 给定如下矩阵
[
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
]
# 输出[1, 2, 3, 6, 9, 8, 7, 4, 5]
简单的方法是模拟整个过程，如蚂蚁一样爬过整个数组，如果遇到边界则右转弯（爬过的部分也算边界）。这个思路比较简单，代码如解法1。 还有一个经典的办法叫做矩阵的ring by ring访问法。显然对于一圈数据的访问我们可以分为4个部分，我们用4 x 4的例子来说明，如下图所示。
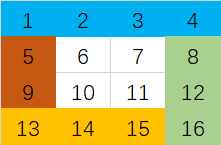
图上有颜色的是一圈数据（一个ring）,蓝色部分是我们要访问的第一个部分，显然其坐标为[0][0, n-1]，绿色是接下来要访问的部分，坐标为[1, m-1][n-1]，接下来是黄色部分[m-1][n-2, 0]，最后是橙色部分，左边为[m-2, 1][0]。显然对于每一个部分我们都是固定一个维度，然后确定另一个维度的上下界，由于每次向内移动一环，上下界也可以确定，只需要每次自增或则自减即可。
class Solution_54:
# 解法1
def spiralOrder(self, matrix):
m = len(matrix)
n = len(matrix[0]) if m else 0
if m == 0 or n == 0:
return []
visit = [[False] * n for _ in matrix]
res = []
# 爬行过程中，先向右，再向下，再向左，最后向上
dirt = [(0, 1), (1, 0), (0, -1), (-1, 0)] # right, down, left, up
i = j = idx = 0
for _ in range(m * n):
res.append(matrix[i][j])
visit[i][j] = True
ni, nj = i + dirt[idx][0], j + dirt[idx][1]
if 0 <= ni < m and 0 <= nj < n and not visit[ni][nj]: # 遇到边界了
i, j = ni, nj
else:
idx = (idx + 1) % 4
i, j = i + dirt[idx][0], j + dirt[idx][1]
return res
# 解法2
def spiralOrder(self, matrix):
m = len(matrix)
n = len(matrix[0]) if m else 0
if m == 0 or n == 0:
return []
res = []
rowu, rowd = 0, m - 1 # 这里可以用一个up, down = m - 1 - up，但是写起来太麻烦
coll, colr = 0, n - 1 # 同上，我喜欢用两个变量标识边界。
while rowu <= rowd and coll <= colr:
for j in range(coll, colr + 1): # [rowu][coll, colr]
res.append(matrix[rowu][j])
for i in range(rowu + 1, rowd + 1): # [rowu+1, rowd][colr]
res.append(matrix[i][colr])
if rowu < rowd and coll < colr:
for j in range(colr - 1, coll, -1): # [rowd][colr-1, colr+1]
res.append(matrix[rowd][j])
for i in range(rowd, rowu, -1): # [rowd, rowu+1][coll]
res.append(matrix[i][coll])
rowu += 1
rowd -= 1
coll += 1
colr -= 1
return res
上面这个题目有两个点比较重要。
- 划分4个部分的时候，一定要有一个部分多一个，比如上述上面的第一部分行比下面第三部分的行多一个，否则最内层（只有一行或者一列，构不成环时）不会被循环到，导致少了一组数据。
- 同样循环时划分一定要准确，否则会对同一个元素多次访问。
类似的题目还有LeetCode 59.
然后回到上面的题目LeetCode 48.这个能不能ring by ring呢，当然可以~。但难点在于定位，完全没有转置在进行翻转的方法直观。(我是想不出来这种解法的)，使用一个4x4的例子来说明。
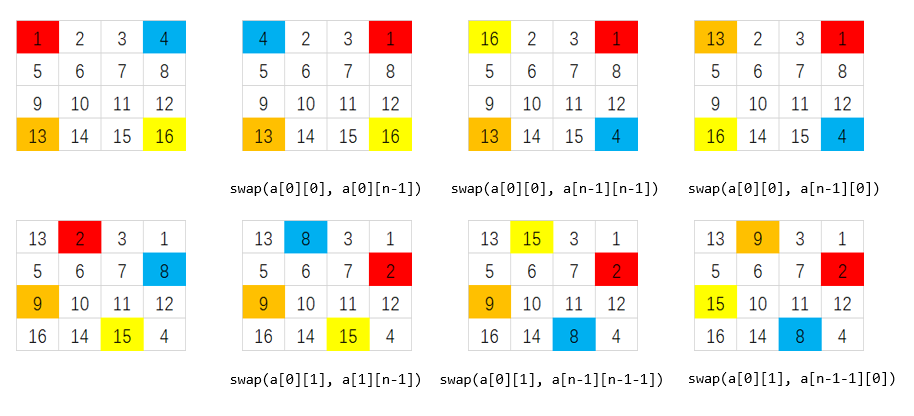如上面一列中，对应四个角的元素不在最终的目标位置上，我们可以通过三次交换（依次与左上角的元素进行交换）来讲他们放到对应的位置上，之后我们将四个位置移动到各自的下一个位置，然后执行同样的（依次与左上角的那个做三次交换），这样四个元素也都移动到了最终的位置，我们依次循环进行下去，直到这一环的元素都被置到确定的位置上。那么什么时候可以确定这一环的元素交换完了呢？答案是与上面ring by ring一样，循环完了左到右的部分（因为是n阶阵，所以四个部分是同步的，用一个循环就能表示这一环）。代码如下：
class Solution_48:
def rotate(self, matrix: List[List[int]]) -> None:
n = len(matrix)
lo, hi = 0, n-1
while lo < hi:
for i in range(hi-lo): # lo + i == hi 表示循环完了这一环
# 三个元素依次与左上角元素交换
matrix[lo][lo+i], matrix[lo+i][hi] = matrix[lo+i][hi], matrix[lo][lo+i]
matrix[lo][lo+i], matrix[hi][hi-i] = matrix[hi][hi-i], matrix[lo][lo+i]
matrix[lo][lo+i], matrix[hi-i][lo] = matrix[hi-i][lo], matrix[lo][lo+i]
# 之后lo自增，hi自减，表示进入内层ring
# 同样可以只是用一个lo来表示，hi = n - 1 - lo.但写起来麻烦
lo += 1
hi -= 1
单链表
对数组右移k位得链表版本LeetCode 61.没啥fancy得技巧，第一遍数节点数n，然后构成环，在一遍数n-k个位置，然后断开（右移k位就是将前n-k个节点摘下来放到后面去）。
class Solution_61:
def rotateRight(self, head: ListNode, k: int) -> ListNode:
if not head:
return head
n = 1
t = head
while t.next:
n += 1
t = t.next
t.next = head
k %= n
if k:
for i in range(n-k):
t = t.next
newh = t.next
t.next = None
return newh
LeetCode 143. 将一个链表得顺序由L0 -> L1 -> … -> Ln得顺序变成L0 -> Ln -> L1 -> Ln-1…依然要求in-place，使用最直观得方法。
- 第一步，使用快慢指针找到中点
- 第二步，将后半段链表反向
- 第三步，合并成目标顺序。
class Solution_143: def reorderList(self, head: ListNode) -> None: """ Do not return anything, modify head in-place instead. """ if not head: return # find the middle node t = p = q = head while p: t = q q = q.next p = p.next if p: p = p.next t.next = None # 断链 # reverse right half mid = ListNode(None) mid.next = q q = mid p = q while p: t = p.next p.next = q q = p p = t # merge p = head while p and q != mid: t = q.next q.next = p.next p.next = q p = q.next q = t题目很简单，都是链表的基本操作，有一些值得注意的小细节。
- 使用快慢指针查找中点时，有时需要取第
n//2,有时需要取第(n+1)//2个。看题目不同，决定要不要使用链头节点。 - 链表翻转的时候最好在纸上画一下示意图，不然容易断链或者构成环。
- 合并循环的终止条件，小心别把链头节点合并进去了（因为后半段使用了链头节点）。
最后讲一个关于链表的环的问题，LeetCode 287.给定一个包含n+1个在区间[1, n]内的数，证明一定至少有一个数重复出现了，假如只有一个重复出现的数，找出这个数。要求：
- 不能修改数组（如果可以修改数组对应于另外一类经典的题目,类似LeetCode 268，LeetCode 41等）
- 空间复杂度O(1)
- 时间复杂度好于O(n²)
- 注意只有一个数重复，但他可能出现多次。
这个题目数据是用数组存储的，但是数据可以当作链表的思想来处理。如给定数组
[1, 3, 4, 2, 2]
链头从下标0开始，可以当作一个链表：
# 1 -> 3 -> 2 -> 4
# ↑____↓
环的入口就是重复出现的数字，因为不能修改数组，就只能使用链表查找环入口的方式。对于链表的查找环的方式为
# 假设 循环链为 A ---> B ---> C
# ^ |
# +------+
# 其中循环的入口点为B，假设快慢指针相遇点是C(C是环上任意一点)
# 第一步，快慢指针同时出发
# 慢指针：A -> B -> C 共N步
# 快指针：A -> B -> ...->C 共2*N步
# 第二步，新指针和慢指针同时不同地出发（如果能够再走N步的话，会是下面这样）
# 慢指针：C -> B -> C 共N步（又走了N步，相当于原快指针，所以会到达C）
# 新指针：A -> B -> C 共N步 (从开头出发，走N步到达C)
# 而实际中由于过程中两个指针同时经过B，这一段的总长度一样为N,
# 后半段B->...->C长度是一样.因此一定在B（循环入口点）点相遇。。
则这道题的代码如下解法1，如果可以修改数组，可以由更简单的方法，如下解法2.
class Solution_287:
# 解法1
def findDuplicate(self, nums) -> int:
slow = fast = nums[0]
# 第一步
while True: # 一定会相遇，所以在循环中break
slow = nums[slow]
fast = nums[fast]
fast = nums[fast]
if slow == fast: # 快慢指针相遇了
break
# 第二步
ptr1 = nums[0]
ptr2 = slow
while ptr1 != ptr2: # 直到第一次相遇，即是环入口
ptr1 = nums[ptr1]
ptr2 = nums[ptr2]
return ptr1
# 解法2
def findDuplicate(self, nums) -> int:
index = nums[0]
# 将对应位置设置为对应的数值，标记为已经访问过，
# 如果已经访问过 index == nums[index] 就找到了环入口
while index != nums[index]:
index, nums[index] = nums[index], index
return index
其他一些链表环的问题LeetCode 141, LeetCode 142。
这一篇涉及到的都是简单的问题，实际做也都可以做的出来，就是数组下标的容易算错，链表操作中容易断链，需要一番debug才能找到问题，实际中还有很多类似得问题，比如上三角矩阵得一维存储，比如链表每k个数为一组进行reverse，以后遇到类似问题要注意：
- 数组问题，想清楚再写，多写一个变量比用个长表达式算舒服多了
- 链表最好画示意图，多操作几次以后就少犯错了
作为基础的两个数据结构，数组和链表应用还很多，其他大多数数据结构都是基于这个来构建，比如基于这两种数据结构的栈和队列的实现（当然这很简单）。
要多锻炼自己徒手写出无bug代码得能力，改掉error-driven得编程习惯，多做题，多总结~