算法总结-字符串匹配
今天来总结一下字符串匹配算法,字符串匹配的问题定义为, 给定:
- 文本串text,长度为n
- 模式串pattern,长度为m,且m<=n
找出text中与patten完全匹配的位置。
解决这个问题的有效算法主要有KMP算法,Rabin-Karp算法和Boyer-Moore算法,当然解决字符串匹配的问题的算法还很多,比如有限自动机,但NFA/DFA写起来太麻烦了(做一道算法题写个自动机杀鸡用牛刀的感觉),查了一些还有名字都没听过的算法,不打算进一步了解了。
暴力算法
首先我们从直观上考虑如何解决这个问题,就是将pattern的开头依次对齐到text串的各个位置来进行匹配,如果出现了失配,我们将pattern移动到下一个位置,从头开始匹配。例如文本串"hello"和模式串"ll"。匹配过程为
h e l l o h e l l o h e l l o
l l l l l l(匹配)
算法代码如下:
def brute_force_match(text, pattern):
n, m = len(text), len(pattern)
for i in range(n-m+1):
j = 0
while j < m and text[i+j] == pattern[j]:
j += 1
if j == m: # a match
return i
return -1
当然这种算法时间复杂度非常糟糕,为O((n-m+1) * m),事实上,暴力匹配的过程中做了很多无意义的匹配,事实上通过对pattern串进行预处理,有效利用pattern串本身的结构可以减少无意义的比较次数。
KMP算法
KMP算法的核心是根据pattern本身求一个部分匹配表(Partial Match Table, PMT)数组,PMT中元素的值是模式串的子串前缀集合和后缀集合交集中最长元素的长度值,整个算法为两个阶段,预处理阶段和匹配阶段。例如
# 一个例子,模式串"abababca":
# index 0 1 2 3 4 5 6 7
# char a b a b a b c a
# PMT 0 0 1 2 3 4 0 1
# next -1 0 0 1 2 3 4 0 1
# 预处理阶段:
# 首先PMT数组的长度和模式串的长度相同,对于上例。
# index=0,串 a 前缀集合{},后缀集合{},交集为{},故PMT[0] = 0
# index=1, 串 ab 前缀集合{a},后缀集合{b}, 交集为{},故PMT[1] = 0
# index=2, 串 aba 前缀集合{a, ab}, 后缀集合{b, ba}, 交集为{a}, 故PMT[1] = 0
# ······
# index=7, 串 abababca 前缀集合后缀集合交集为{a}, PMT[7] = 1
# 匹配阶段:
# 然后有了PMT数组之后,我们就能进行匹配过程,如对文本串"ababababca",
# a b _a_ _b_ _a_ _b_ [a] b c a i = 6
# _a_ _b_ _a_ _b_ a b [c] a j = 6
# 当i=6, j=6是第一次出现失配(中括号对应得字符不相同),而这是[i-j, i-1]与[0, j-1]是
# 已经匹配过的完全相同得子串部分,而这一模式串得子串pattern[:j] = "ababab" 中有相同的
# 前后缀abab,长度为PMT[j-1] = 4, 对应就是上面下划线包围部分的字符是对应匹配的,不需要
# 再重复比较。直接将pattern串移动到PMT[j-1]与i进行匹配即可(i不需要移动)。
实际编程中,为了方便,通常将PMT数组右移一位,并将0位置设为-1(只是为了方便,下面代码可以看到,使用-1可以带来代码的方便),记为next数组,当出现失配时,将j移动到next[j]继续匹配。
接下来要解决怎么计算next数组(或计算PMT数组)的问题,我们可以按照定义,枚举出模式串的子串pattern[0:j]的所有前后缀然后找出交集并取最长元素的长度,但注意到,求next数组,是找模式串中前缀与后缀匹配的长度,因此,这也是一个字符串匹配的过程,即:以pattern[1:m-1]为文本串,以pattern[0, m-2]为模式串的字符串匹配过程。一旦字符串匹配成功,那么当前的next值就是匹配成功的字符串的长度。
因此整个KMP的算法的过程如下:
def KMP_match(text, pattern):
def cal_next(p):
"""预处理,计算next数组"""
next = [0] * (len(p) + 1) # 注意next数组长度是m+1
next[0] = -1
# 初始化i=1,j=-1这样从模式串(i=1, j=0)开始匹配(会执行一遍i++,j++)
# 即保证前缀p[0, m-2] 和 后缀p[1:m-1] 匹配
i, j = 0, -1
while i < len(p):
# -1的作用:
# 1. 实现前缀与后缀匹配
# 2. 出现失配i移动到i+1, j移动到0
if j == -1 or p[i] == p[j]:
i += 1
j += 1
next[i] = j
else:
j = next[j]
return next
def kmp(text, p):
"""匹配过程"""
i = j = 0
next = cal_next(p)
while i < len(text) and j < len(p):
if j == -1 or text[i] == p[j]: # -1的作用,如果出现了-1,就是next[0],
i += 1 # 说明模式串第一字符就不匹配,i和j都右移一位
j += 1 # i移动到了i+1, j+1移动到了0,即从头开始
else:
j = next[j]
if j == len(p): # a match
return i - j
return -1
return kmp(text, pattern)
Boyer-Moore 算法
同KMP算法一样,BM的算法思想也是基于对pattern串的预处理来减少重复的匹配,不同之处在于,BM算法是逆序匹配/从右向左匹配,即对模式串是从m-1匹配到0,在减少重复匹配上,BM算法主要使用了两个启发思想:
- 坏字符
- 好后缀
这对应两个向后的移动数组(类似KMP中的next数组)bmBC和bmGS,然后我们每次出现失配时,我们从中选能移动的更多的那一个(即避免更多无意义比较)。
下面我们使用来自[2]中的例子来说明这两个思想。
text = "HERE IS A SIMPLE EXAMPLE"
pattern = "EXAMPLE"
首先来看坏字符。坏字符的思想比较简单,就是出现失配的字符,当在位置i出现失配时,坏字符就是text[i]。如下,此时的坏字符是text[6]='S'。
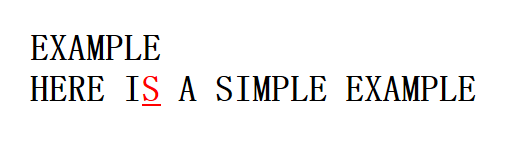
显然此时,模式串中不含有坏字符S,因此我们可以直接右移整个模式串,移动字符个数为 m。移动后如下。
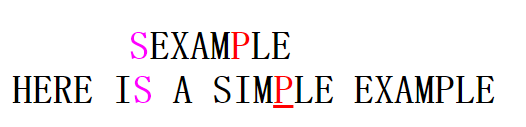
此时新的坏字符为P,这是我们需要将模式串pattern右移,那么具体右移多少个字符呢? 思考从右向左的匹配的过程中,如果匹配,则有text[i] == pattern[j],就是当前的坏字符一定与模式串的某一个位置中的字符相同,这样,我们可以将模式串右移到最右边出现的坏字符与i位置对齐(不进行左移的提前下)。移动的字符个数是:坏字符位置 - 坏字符在模式串中上一次出现的位置,如上例子中,移动字符个数 6-4=2。
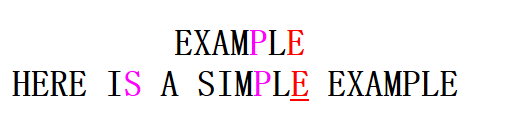
计算坏字符移动数组bmBC,我们将要移动字符的个数存储在数组中。对此,我们需要记住每个字符最右边的位置到字符串尾的字符个数,简单的方式是每次循环从模式从右边往左边找就好了,可是模式串长了这样很耗时。我们使用空间换时间的做法,直接使用字符作为下标(char 才128个,即使unicode我们也可以使用hash table),这样计算过程就非常简单。
def pre_bad_ch(p):
"""坏字符"""
m = len(p)
bmbc = [m] * 128 # 初始化为m, 没出现的字符移动整个串的长度
# 出现的移动长度为m - 1 - k(k到字符串尾的长度), 从左到右循环,后面出现
# 的会覆盖前面出现的值,最终保留下来就是最右边出现的对应移动值。
for k in range(m - 1):
bmbc[ord(p[k])] = m - 1 - k
return bmbc
再来看好后缀思想,因为是从右到左匹配的,当前部分匹配的是一个模式串的后缀。如果在匹配了一部分之后出现了失配,这是我们有了一个匹配好的后缀(好后缀),如果模式串中还有一个与好后缀相同的子串,或者模式串的一个前缀与好后缀的部分后缀相同的话,那么可以把与好后缀相同的子串(或者与好后缀的后缀相同的模式串前缀)移动到当前位置。继续上述例子的匹配过程的话我们有

这时的好后缀是MPLE,模式串中不存在与其完全相同的另一个子串,但是存在一个前缀pattern[0:1] = "E"与好后缀的后缀部分"E"相同,因此我们可以进行如下移动。
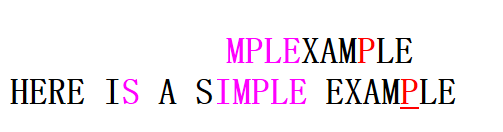
好后缀的细节比较复杂,我们把它细分一下,有三种情况[3]。
1、模式串中有和好后缀完全相同的子串,那么将最右的子串移动到好后缀的位置,移动的长度是:前面子串出现的位置(用最后一个字符下标表示)到字符串尾的长度
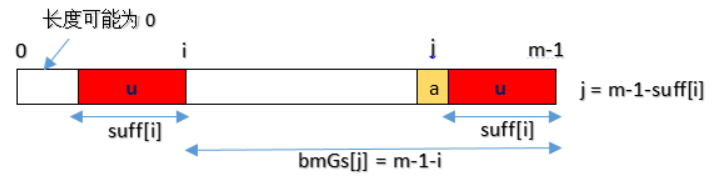 2、如果有和好后缀的部分后缀相同模式串前缀,那么将这个前缀移动到当前位置,移动的长度是:前面前缀出现的位置(用前缀最后一个字符下标表示)到字符串尾的长度
2、如果有和好后缀的部分后缀相同模式串前缀,那么将这个前缀移动到当前位置,移动的长度是:前面前缀出现的位置(用前缀最后一个字符下标表示)到字符串尾的长度
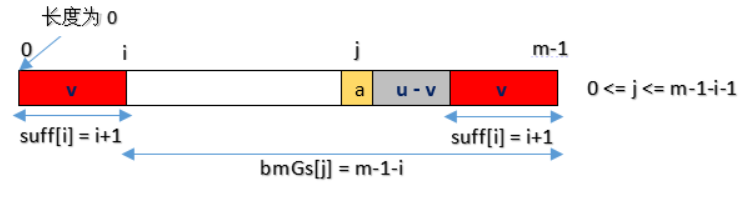 3、不存在与好后缀/好后缀后缀相同的子串,右移整个模式串。
3、不存在与好后缀/好后缀后缀相同的子串,右移整个模式串。
接着要思考怎么计算好后缀移动数组的bmGS,为了计算bmGS,我们需要使用一个辅助数组suff,suff[i]表示在pattern[:i+1]中后缀与与模式串后缀的交集的元素的最长值(等会儿再来具体说明)。对应上述三种情况,计算好后缀移动数组bmGS的过程如下。
def pre_good_suffix(p, suff):
m = len(p)
# 依然初始化为m。
# 处理上述 情况3. 没有与后缀相同的子串或者前缀
bmgs = [m] * m
# 对于 情况2. 有前缀和好后缀一致,即:p[m-s:m] == p[0, s],
# 我们可以将这个前缀视为已匹配的部分,将模式串移到这个前缀与好后缀的后面对齐的位置。
j = 0
for k in range(m - 1, -1, -1):
if suff[k] == k + 1: # 与后缀相同的长度k+1说明是模式串的一个前缀
while j < m - 1 - k:
# 移动字符的个数是前缀的位置(用k表示)字符串尾部的长度(m-1 - k)。
# TODO:这里我看好多代码都加了一个判断bmgs[j]==m,比如参考文献[4],
# 可是我觉得好没有必要
bmgs[j] = m - 1 - k
j += 1
# 情况1,有子串与好后缀一致。对应j=m-1-suff[k]
for k in range(m - 2 + 1):
j = m - 1 - suff[k]
bmgs[j] = m - 1 - k
return bmgs
然后再来说怎么得到suff数组,根据它的含义:在pattern[:i+1]中后缀与与模式串后缀的交集的元素的最长值,我们可以直接暴力求解。
def suffix_brute_force(pattern):
m = len(pattern)
suff = [0] * m
suff[m - 1] = m
for i in range(m - 2, -1, -1):
j = i
while j >= 0 and pattern[j] == pattern[m - 1 - i + j]:
j -= 1
suff[i] = i - j
return suff
同样我们也可利用已经计算过的suff的值,来加速这个计算过程,原理解释参考[3]。
def suffix(pattern):
m = len(pattern)
suff = [0] * m
suff[m - 1] = m
f, j = 0, m-1
for i in range(m - 2, -1, -1):
if i > j and suff[i + m - 1 - f] < i - j:
suff[i] = suff[i + m - 1 - f]
else:
# j = min(j, i)
if i < j:
j = i
f = i
while j >= 0 and pattern[j] == pattern[j + m - 1 - f]:
j -= 1
suff[i] = f - j
return suff
有了以上的所有准备,我们就可以开始进行匹配了,。
def BM_match(text, pattern):
n, m = len(text), len(pattern)
bmbc = pre_bad_ch(pattern)
bmgs = pre_good_suffix(pattern)
print('bc', bmbc[ord('a'):])
print('gs', bmgs)
j = 0
while j <= n - m:
i = m - 1
while i >= 0 and pattern[i] == text[i + j]:
i -= 1
if i < 0: # 一个完整的match, 多次匹配可以记下结果并j += bmgs[0]
return j
else:
# BM算法的核心,每次从两种思想中移动距离长的一个
j += max(bmbc[ord(text[i + j])] - m + 1 + i, bmgs[i])
return -1
Rabin-Karp算法(Rolling Hash)
Rabin-Karp算法通过将字符串视作一个字符集数目进制的数(实际代码中常取一个并字符集个数多的素数),然后这个数目的值会很大,所以要对一个比较大的素数取模。然后通过比较数,数相同了再去比较字符串是否相同。
其关键思想在于,对一个字符串s[:n]我们有hash(s) = (s[0] * P^(n-1) + s[1] * P^(n-2) + s[2] * P^(n-3) + ...,+ s[n-1] * p^0) % MOD,其中p和MOD是两个素数。这样hash(s)的值被比较均匀的散列到[0, MOD-1],然后如果对于两个字符串散列值相同的话,字符串也有很大可能相同。
对于hash值计算,假如有了hash(s),现在想计算向后滚动一个字符的位置,我们可以首先从hash中减去s[n-1] * p^(n-1),我们就得到了hash(s[:n-1]),然后加上一个新字符 c * p ^ (0) 再对MOD取模。即得到了hash[s[1:n+1]]。
直接给出算法代码如下.
def match(text, pattern):
def check(s, t):
if len(s) != len(t):
return False
for i in range(len(s)):
if s[i] != t[i]:
return False
return True
n, m = len(text), len(pattern)
if n < m:
return -1
if m == 0:
return 0
MOD = int(1e9+7)
p = 113
h = p ** (m - 1) % MOD
code = lambda c: ord(c) - ord('a')
target = cur_val = 0
for i in range(m):
target = (target * p + code(pattern[i])) % MOD
cur_val = (cur_val * p + code(text[i])) % MOD
if cur_val == target and check(text[:m], pattern):
return 0
for i in range(m, n):
cur_val = ( (cur_val - code(text[i-m]) * h) * p + code(text[i])) % MOD
# hash值相同,检查串是否相同
if cur_val == target:
if check(pattern,text[i - m + 1:i + 1]):
return i - m + 1
return -1
这些知识基础的字符串匹配算法,实际使用中如果不是要求实现这几种算法,那么使用像是python的str.index()和str.find()或者c++中的find,rfind等就足够了,理解这些算法的意义在于灵活运用,比如LeetCode 796. 判断一个字符串是不是原字符串rotate之后得到,我们可以使用暴力方法依次旋转来比较,但是这样时间复杂度是O(n²),我们可以使用Rabin-Karp算法,能够将时间复杂度降低到O(n)。同时,字符串匹配远不止这些内容,比如字符串正则匹配就可以使用动规来解。(忘记了在哪看到了一句话,字符串题90%都可以用动规,害怕)。
多做题,多总结~
参考文献
[0]. 算法导论Thomas H.Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein.
[1]. https://www.zhihu.com/question/21923021/answer/281346746
[2]. http://www.cs.utexas.edu/~moore/best-ideas/string-searching/fstrpos-example.html
[3]. https://www.cnblogs.com/ECJTUACM-873284962/p/7637875.html
[4]. http://www-igm.univ-mlv.fr/~lecroq/string/node14.html
[5]. http://zh.wikipedia.org/wiki/%E6%A8%A1%E5%8F%8D%E5%85%83%E7%B4%A0