来总结一下DQN以及他的各种变种。DQN是Valued Based, Model-free, off-policy, TD方法。自提出来就出现了许许多多的改进版本,这里有个总结，虽然不太完全，但中间有个DQN存在问题的list很精准，不过文章没有对每一个改进进行详细的分析。本文参考了刘建平Pinard的博客

TODO

notations不一致
algos 用的都是图片，框架不太一样，不好看

Q-Learning

DQN由Q-Learning发展而来，先来回顾一下Q-Learning.

Q-Learning主要是通过学习动作价值函数Q来直接近似求的最优动作价值函数Q*。动作价值函数Q定义为：

\[Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha[R_{t+1} + \gamma \max_a Q(S_{t+1}, a) - Q(S_t, A_t)]\]

其中，$\delta = Q_{target} - Q(S_t, A_t) = R_{t+1} + \gamma \max_a Q(S_{t+1}, a) - Q(S_t, A_t)$是TD-error。Q-Learning的算法为图片来自RL: An introduction

DQN

Q-Learning使用表格法来表示状态动作价值函数，这对于状态比较少的情况没什么问题。但现实是很多问题的状态太多了,这时候深度学习就有用了。使用Value Fucntion Approximation. NIPS 2013版本的DQN就是使用神经网络代替了Q-Learning中的表格，同时使用了经验回放机制。训练神经网络需要有一个优化的目标函数，即Loss函数，而我们可以直接利用Q-Learning中的减小TD-error的思想，将Loss函数定义为： $L(\theta) = \mathbb{E}[(\delta)^2] = \mathbb{T}[(Q_{target} - Q(s, a;\theta))^2]$

对其求梯度为： $\nabla_{\theta_i}L_i(\theta_i) = \mathbb{E}[(r+\gamma\max_{a'}Q(s', a';\theta_{i-1})- Q(s, a;\theta_i)) \nabla_{\theta_i}Q(s, a;\theta_i)]$

图片来自^[Mnih V, Kavukcuoglu K, Silver D, et al. Playing atari with deep reinforcement learning[J]. arXiv preprint arXiv:1312.5602, 2013.]

算法中equation 3就是上面的梯度公式。除了使用神经网络来近似Q之外， NIPS DQN使用了经验回放机制，就是将每一步与环境交互收集的数据存放到中经验池中，每次从经验池中随机采样一部分数据，用这部分数据使用梯度方法更新Q网络，这种做法降低了数据样本的相关性。

Nature DQN

NIPS DQN只使用了一个Q网络，而且计算$Q_{target}$的过程中，使用了到了即将被更新的网络： $Q_{target} = \left \{ \begin{aligned} & r_t, \qquad \qquad \qquad terminal \space s_{t+1} \\ & r_t + \gamma max_{a'}Q(s_{t+1}, a'; \theta), \quad nonterminal \space s_{t} \end{aligned} \right.$

这样导致一个问题就是我们使用这个网络算出的target来更新这个网络的参数，这样两者强相关，会影响网络的收敛性。

Nature DQN通过使用另外一个相同结构的target网络来改善这个问题。使用一个网络用来产生动作的Q值，和更新网络的参数（我们把这个叫做eval网络），另一个target网络只用来计算$Q_target$，参数隔一段时间从eval网络拷贝一次，由于target网络并不参与训练，所以切断了NIPS DQN中只有单网络的相关性。

除了多了一个target网络之外，Nature DQN与NIP DQN算法其他部分完全相同，算法如下。

图片来自^[Volodymyr Mnih, et al. Human-level control through deep reinforcement learning. Nature 518.7540 (2015): 529.]

DDQN

前面DQN中，我们希望能够快速的收敛到优化目标，最大化我们获得的累计reward，计算$Q_{target}$的时候使用都是对取下一个状态的最大动作价值$\max_{a’}Q(s_{t+1},a’)$，但是这样容易产生过估计（over estimation）问题。过估计的原因是： [^_^]: <这里的notation 要改一下="">

\[E[\max(y_1, y_2, y_3,...)] \ge \max (E[y_1, y_2,...])\]

这个式子很简单，就是对一系列数先求最值再求期望会大于等于期望的最值。强化学习中的目标是要最大化累计reward的期望（期望的最值），而在上述DQN中求取的相当于是最值的期望，也就产生了Q值的估计比实际要大，最终得到的Q函数会有很大的bias。

为了解决这个问题，Double-DQN的idea就是引入另外一个网络，将求$Q_{target}$过程中的$\max_a$这一步进行解耦。 $\begin{aligned} Q_{target} &= R_{t+1} + \gamma \max_a Q'(S_{t+1}, a) \\ &= R_{t+1} + \gamma Q'(s_{t+1}, \argmax_{a'}Q(s_{t+1}, a')) \\ \end{aligned}$

实际上在Nature DQN中，我们已经有了两个网络，所以可以直接利用起来，上面的公式也正是这样。简单来说，就是DDQN在计算target时，不是直接取最大值，而是使用eval网络算出下一个动作，然后使用这个动作放到target网络中算target值。

Prioritized Replay DQN

这个算法关注经验回放的问题。在人类学习的经验中，有些经验是比另外一些经验更重要的，也就是过去的经验对学习的效果有着不同的重要性，强化学习中也是这样。而在前序的一些工作中，我们将与环境交互产生的数据一股脑地存放到经验池中，然后再等概率的进行采样拿去训练我们的Q网络，但有可能采样到的对Q网络带来的更新不大，因此网络收敛会很慢。显然，我们应该以不同的优先级对经验池中的数据进行采样，那什么样的数据对我们更重要呢？回想一下上面讲过我们的优化目标是最小化(TD-error)²，TD-error的绝对值越大（loss越大）对我们网络的更新幅度越大。这样，我们应该倾向于采样那些|TD-error|比较大的经验数据。因此我们使用优先级机制来从经验池中采样，同时存储经验的时候也应该指定其优先级为TD-error的绝对值。实际应用中经常使用sumTree数据结构来存储replay。 [^_^]: there is a lot to talk about.

图片来自^[Schaul T, Quan J, Antonoglou I, et al. Prioritized experience replay[J]. arXiv preprint arXiv:1511.05952, 2015.]

使用了带优先级的经验回放之后收敛速度要大幅优于其他的DQN，而且可以和其他的DQN方法结合，上述算法就是带优先级经验回放的DDQN。

Duel DQN

CV中经常使用新的网络结构，就出现了奇迹般的效果，强化学习中也有这么做的。首先看一个定义，advantage函数： $A(s, a) = Q(s, a) - V(s)$

之后还会多次遇到这个函数，实际上它是这么来的 $Q(s, a) = V(s) + A(s, a)$。即将动作价值函数分成了与只与状态有关的状态价值函数$V(s)$和动作的优势函数A(s, a)。我们将其参数化为： $Q(s,a;\theta, \alpha, \beta) = V(s; \theta, \alpha) + A(s,a; \theta, \beta)$

原文中说，根据这个式子得出$V(s;\theta,\alpha)$是状态价值函数的一个很好的估计这样的结论是错误的。同样也不能认为$A(s,a; \theta, \beta)$提供了有效的优势函数的估计。（为什么？因为并没有提供V/A的label对A进行估计，实际上V/A可以看作估计Q的过程中的隐含参数？例如，V的估计比实际大了一个常量值，而A的估计比实际小了同样的常量值，这样Q是一样，而V/A估计都不正确。）

在神经网络的结构中，将这两个部分分别输出然后再联合起来输出动作价值函数Q。网络结构对比如下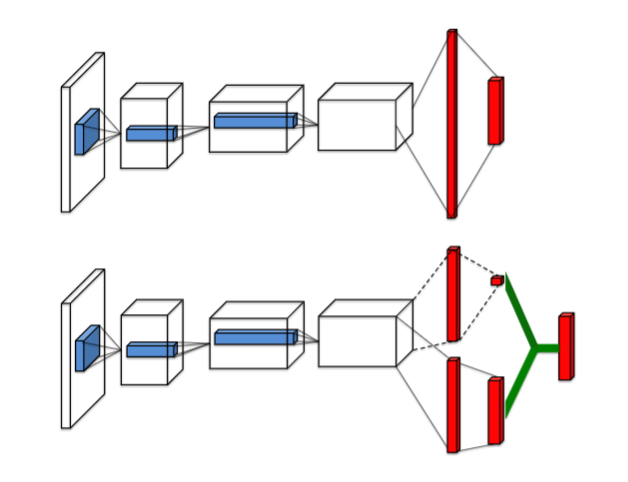：图片来自^[Wang Z, Schaul T, Hessel M, et al. Dueling network architectures for deep reinforcement learning[J]. arXiv preprint arXiv:1511.06581, 2015.]，传统Q网络结构（上），Duel-DQN网络结构（下）

这里如果直接使用加和的方式来得到Q，就和传统的方法没什么区别（给两个隐含变量取了名字而已），根本无法区分最终输出里V和A起到的作用。要利用起着这种网络结构，必须想方设法区分V和A这两块,实际使用的方式是： $Q(s,a;\theta, \alpha, \beta) = V(s; \theta, \alpha) + (A(s,a; \theta, \beta) - \frac{1}{\mathcal{A}}\sum_{a' \in \mathcal{A}}A(s,a'; \theta, \beta))$

DRQN

既然网络结构可以twist了，那加入RNN会怎么样。主要再原有DQN的Q网络结构后面加了一层LSTM，用来解决partially obsevation情况下（MDP变为POMDP）。有一个冲突是LSTM善于处理序列数据，所以应该一次使用一个trajectory来训练，而DQN中为了避免相关性将数据存入经验池，之后随机采样数据来训练。文章试验了序列化更新和随机采样更新，效果差不多。除了网络结构的差异，其他和DQN差不多。

Rainbow DQN

deepmind大佬做的DQN大杂烩 Double + Prioritized Replay + Dueling + Distribution + Noisy + Multi-step(n-step boostrappping)。基本上就是结合以上几种方法，发现差不多是互补的在大多数任务上表现都好的多。

参考文献

[1]. Reinforcement Learning: An Introduction,Sutton, R.S, Barto, A.G [2]. Mnih V, Kavukcuoglu K, Silver D, et al. Playing atari with deep reinforcement learning[J]. arXiv preprint arXiv:1312.5602, 2013 [3]. Volodymyr Mnih, et al. Human-level control through deep reinforcement learning. Nature 518.7540 (2015): 529. [4]. Schaul T, Quan J, Antonoglou I, et al. Prioritized experience replay[J]. arXiv preprint arXiv:1511.05952, 2015. [5]. Wang Z, Schaul T, Hessel M, et al. Dueling network architectures for deep reinforcement learning[J]. arXiv preprint arXiv:1511.06581, 2015.