推荐系统 CTR 模型总结
一些问题
- 对输入的处理过程
- DeepFM 不是共享 embedding 吗,DeepCTR 我看好多特画图都是把线性和 DNN 部分的 Embedding 分开画的。
- Feature Hashing?
impression: 显示 click: 点击 CTR: click / impression
RS
概念
根据用户的不同特征,想用户个性化的推荐物品 (Item) 的系统。
搜索,推荐,广告都是在解决信息过载问题。
对于搜索来说,本质要根据用户 Query 给出精准的结果 对于广告来说,本质要解决广告主,用户,媒体三分的利益协调问题 对于推荐来说,本质要优化用户体验,也即是个性化
| 搜索 | 广告 | 推荐 | |
|---|---|---|---|
| 用户信息获取方式 | 主动 | 被动 | 被动 |
| 点击率要求 | 有 | 有 | 有 |
| 惊喜度要求 | 无 | 无 | 有 |
| 个性化要求 | 可能 | 可能 | 有 |
| 用户反馈 | 隐性为主 | 隐性为主 | 隐性/显性 |
| 关注点 | 内容消费方 | 内容生产方 | 内容生成方消费方 |
| 是否需要集体智慧 | 可能 | 需要 | 可能 |
| 是否需要 Query | 需要 | 可能 | 可能 |
| 是否依赖上下文 | 可能 | 可能 | 可能 |
推荐目的是为了:
- 帮助用户找到想要的物品(Item),发掘长尾(长尾理论,指热门的小部分资源得到了大部分关注,剩下的大部分资源鲜有人问津)
- 降低信息过载
- 提高站点点击率/转化率
- 加深对用户的理解,个性化/定制化
点击率 CTR(click-through rate)和转化率CVR(conversion rate)是衡量广告流量的两个关键指标。准确的估计CTR、CVR对于提高流量的价值,增加广告收入有重要的指导作用。
点击率 CTR 预估的关键在于学习组合特征。注意,组合特征包括二阶、三阶甚至更高阶的,阶数越高越复杂,越不容易学习。Google 的论文研究得出结论:高阶和低阶的组合特征都非常重要,同时学习到这两种组合特征的性能要比只考虑其中一种的性能要好
召回(match)”指从全量信息集合中触发尽可能多正确的结果,并将结果返回给“排序”,它可能包含来源于渠道,比如协同过滤、主题模型、内容召回和热点召回等渠道,能够从内容库中选出多样性的偏好内容。注重性能要求。
由于没有 Query ,所以推荐系统召回面临的是全量信息池,需要根据用户画像、内容画像等各种信息,从整个信息集合中挑选除尽可能多的相关结果,剔除相关性较弱的结果,降低排序阶段的工作量。
关于什么样的召回策略是好的,评价指标 召回率和精度 Recall = 检测到的相关内容 / 所有的相关内容 (TP / (TP + FN)) Percision = 检测到的相关内容 / 检测到的所有内容 (TP/ (TP + FP))
基于内容匹配的召回
内容匹配即用户画像和内容画像进行匹配,包括基于内容标签的匹配和基于知识的匹配。 Recall 较高,Percision 较低,(会召回大量结果,同时包含了大量不相关的 FP)
基于协同过滤的召回
基于用户(User-based)的协同过滤 是最基础的,发现相似用户,把一个用户的内容推送个另一个相似用户。 基于项目(Item-based)的协同过滤 计算 Item 之间的相似性,根据用户历史来推荐 基于模型(Model-based)的协同过滤 基于样本的用户喜好,训练一个推荐模型,然后用这个模型预测。
Percision 较高(检测到的内容中不相关(FP)比较少),但存在冷启动问题。
关于冷启动
- 推荐主体冷启动(新用户)
- 扩充画像
- 注册信息(年龄,性别,手机号,LBS)
- 社交账号登陆
- 标签预采集
- 数据交互
- 新建推荐逻辑
- 推荐热点(热点很大概率错不了)
- Bandit 算法(Expolitation & Exploration)
- 扩充画像
- 被推荐对象冷启动(Item)
- ICF 聚类
- 自身属性分析
- 系统冷启动(全新系统,只能靠专家经验)
推荐中的模型评估
按照推荐任务不同,常用的推荐度量方法分为三类:
- 对预测的评分进行评估,适用于评分预测任务
- 对预测的 Item 集合进行评估,适用于 Top-N 推荐任务
- 按排名列表对推荐效果加权进行评估,既可以适用于评分预测任务也可以用于 Top-N 任务
评分预测指标: 如准确度指标:平均绝对误差(MAE),均方误差根(RMSE),标准化平均误差(NMAE)等;和覆盖率(Coverage)
集合推荐指标: 精度(percision),召回(Recall),ROC & AUC
排名推荐指标: half-life, discounted cumulative gain.
CTR 模型
传统的 CTR 模型采用的是 特征工程 + LR/FM 的方法,大量的特征工程的工作费时费力。深度 CTR 是将深度学习应用到 CTR 中,深度 CTR 一般具有:【输入】,【Embedding】,【特征交互】,【输出】四个模块。
矩阵分解
推荐系统中,很重要的一点就是用户对商品的打分数据,这是一个用户打分的稀疏矩阵。有一类问题就是预测用户对未打分的商品进行评分预测。
记评分矩阵为 $R_{m \times n}$,使用矩阵分解,将其分解成两个矩阵 $P_{m\times k} , Q_{k \times n}$,我们要使得分解后的矩阵能够还原元素的矩阵 $R_{m \times n}$。即
\[R_{m \times n} \approx P_{m \times k} \times Q_{k \times n} = \hat{R}_{m \times n}\]求解矩阵 $P_{m\times k} , Q_{k \times n}$ 中的每一个元素可以当作一个回归问题来求解。优化目标为: \(\begin{aligned} \underset{}{\min} &\sum_{r_{ij} \ne \textrm{NaN}} e_{ij}^2 \\ e_{ij} &= (r_{ij} - \hat{r}_{ij})^2 = (r_{ij} - \sum_{k=1}^{K} p_{ik} q_{kj})^2 \\ \end{aligned}\)
然后使用梯度下降求解就可以了。
另外,为了提高泛化能力,会在损失函数中加入正则项。 \(e_{ij} = (r_{ij} - \sum_{k=1}^{K} p_{ik} q_{kj})^2 + \frac{\beta}{2} \sum_{k=1}^{K}(p_{ik}^2 + p_{kj}^2)\)
LR(参见机器学习部分)
用于 CTR 预测,用户点击/不点击作为二分类问题,对嵌入后的特征进行简单加权求和后经过一个 Sigmoid 函数得到输出,主要是逻辑回归简单易于实现且有效,但需要大量的人工特征。
LR 的并行化 两种方式
- 按行并行:将样本划分到不同的机器上去,求得梯度,然后归并求梯度平均,更新参数。
- 按列并行:将样本按照特征分到不同的机器上去,求得部分特征的梯度,然后合并为整体的梯度,更新参数。
MLR(Mixed Logistic Regression)
FM(因子分解机)
[排序],召回,排序的利器。
解决稀疏数据下的特征组合问题
- 数据高度稀疏场景
- 具有线性的计算复杂度
与 LR 相比,FM 增加了二阶项的信息,通过穷举所有的二阶项并结合权重来预测。使用组合特征是因为两个特征关联之后与要预测的结果之间相关性会提高。
最直观的是使用多项式模型。二阶的表达式如下:
\[f(x) = \underbrace{ w_0 + \sum_{i=1}^{n} w_i x_i} + \underbrace{ \sum_{i=1}^{n} \sum_{j=i+1}^{n} w_{ij} x_i x_j }\]其中,$n$ 代表样本特征的数量,$x_i$ 是样本第 $i$ 个特征的值,$w_0, w_i, w_{ij}$ 是模型参数。
显然,前半部分就是 $wx+b$ 线性部分,最后一项是二阶交叉项,从模型看,FM 表达能力强于 LR 。
由公式可以看出,组合特征的数目为 $n(n-1)/2$ ,如果 n 本身很大,组合特征数目会特别多,样本特别稀疏,而 $x_i x_j$ 非零的项会非常少,而对于观察样本中未出现的过交互的特征分量,无法对参数进行估计,从而导致训练样本不足,容易导致参数不准确,严重影响模型性能。
为了克服上面高度稀疏带来的无法训练的问题,我们可以考虑:所有的二次项参数 $w_{ij}$ 都可以组成一个对称矩阵 $W$ ,其可以分解为 $W = V^TV$ ,V 的第 j 列便是第 j 维特征的隐向量(引入的辅助向量,维度 k 是超参),也即是参数 $w_{ij} = v_i \cdot v_j$ ,于是有
\[f(x) = w_0 + \sum_{i=1}^{n} w_i x_i + \sum_{i=1}^{n} \sum_{j=i+1}^{n} (v_i \cdot v_j) x_i x_j\]那么,任意给定一个矩阵二次项参数矩阵 $W$ 是否能够找到相应的分解 $V$ 呢?当 $k$ 足够大时,对于任意正定的实对称矩阵,$W \in R^{n\times n}$ ,均存在实矩阵 $V \in R^{n \times k}$ ,使得 $W = V^TV$ 成立。
显然 $W$ 是对称的,那么如何保证正定呢?注意到,我们只关心不同特征量之间的关系,所以对于 $W$ 的对角线元素我们可以任意取值,只要取得足够大,就可以保证其正定。
直观上讲,FM 的复杂度是 $O(kn^2)$ 其中 $k$ 是隐向量 v 的长度,但是可以通过以下化简,将复杂度优化到 $O(kn)$ 。
由于 $V^TV$ 是对称的,所以 $v_i \cdot v_j = v_j \cdot v_i$ ,而 $\sum_{i=1}^{n} \sum_{j=i+1}^{n} (v_i \cdot v_j) x_i x_j$ 是上三角部分,因此有:
\[\begin{aligned} \sum_{i=1}^{n} \sum_{j=i+1}^{n} (v_i \cdot v_j) x_i x_j &= \frac{1}{2} \left( \sum_{i=1}^{n} \sum_{j=1}^{n} (v_i \cdot v_j) x_i x_j - \sum_{i=1}^{n} (v_i \cdot v_i) x_i x_i \right) \\ &= \frac{1}{2} \left(\sum_{i=1}^{n} \sum_{j=1}^{n} \sum_{f=1}^{k} v_{i,f}v_{j,f} x_i x_j - \sum_{i=1}^{n} \sum_{f=1}^{k} v_{i,f}^2 (x_i)^2 \right) \\ &= \frac{1}{2} \sum_{f=1}^{k} \left[ \left( \sum_{i=1}^{n} v_{i,f} x_i \right) \left( \sum_{j=1}^{n} v_{j,f} x_j \right) - \sum_{i=1}^{n} v_{i,f}^2 x_i^2 \right] \\ &= \frac{1}{2} \sum_{f=1}^{k} \left[ \left( \sum_{i=1}^{n} v_{i,f} x_i \right)^2 - \sum_{i=1}^{n} v_{i,f}^2 x_i^2 \right] \\ \end{aligned}\]这样计算的复杂度就变成了 $O(kn)$ 。
如果使用 SGD 各个参数的梯度如下:
\[\frac{\partial f(x)}{\partial \theta} = \left \{ \begin{aligned} &1 &;\textrm{if }\theta\textrm{ is }w_0 \\ &x_i &;\textrm{if }\theta\textrm{ is }w_i \\ &x_i\sum_{j=1}^{n} v_{j,f}x_j - v_{i,f} x_i^2 &;\textrm{if }\theta\textrm{ is }v_{i,f} \end{aligned} \right.\]FM 可以扩展到高阶,但是由于复杂度太高,所以很少使用。
FFM
对 FM 增加了 field 概念。简单来说,同一个categorical特征经过One-Hot编码生成的数值特征都可以放到同一个field,包括用户性别、职业、品类偏好等。对每一维特征 $x_i$ ,针对其他特征的每一种 field $f_i$ ,都会学习一个隐向量 $v_{i,f_j}$,即隐向量既与特征有关,又与 field 有关。
设 n 个特征属于 f 个 field。
\[f(x) = w_0 + \sum_{i=1}^{n} w_i x_i + \sum_{i=1}^{n} \sum_{j=i+1}^{n} (v_{i, f_j} \cdot v_{j,f_i}) x_i x_j\]FFM 二次项不能优化,复杂度 $O(n^2)$。
学习使用的是 logistic loss, 同时添加了 L2 正则。
\[min_w \sum log(1 + e^{-y_i f(x_i|w)}) + \frac{\lambda}{2} \| w \|^2\]一些细节:
- 样本归一化,避免梯度 nan
- 特征归一化,数值型特征归一化到 [0, 1]
- 省去零值特征
CCPM
FNN
FM 预训练的向量输入到 MLP 中,输出预测。
PNN
Product-based NN。显性的在 embedding layer 之后添加了 Product 层,用来捕捉二阶特征相关性。
DNN 应用在 CTR 中经常是 Embedding + MLP 结构,通常 NN 层之间使用 add op 并且通过激活函数来引入非线性。PNN 作者认为单纯 add 不足以捕获不同 field 特征之间的相关性,由此引入 PNN。
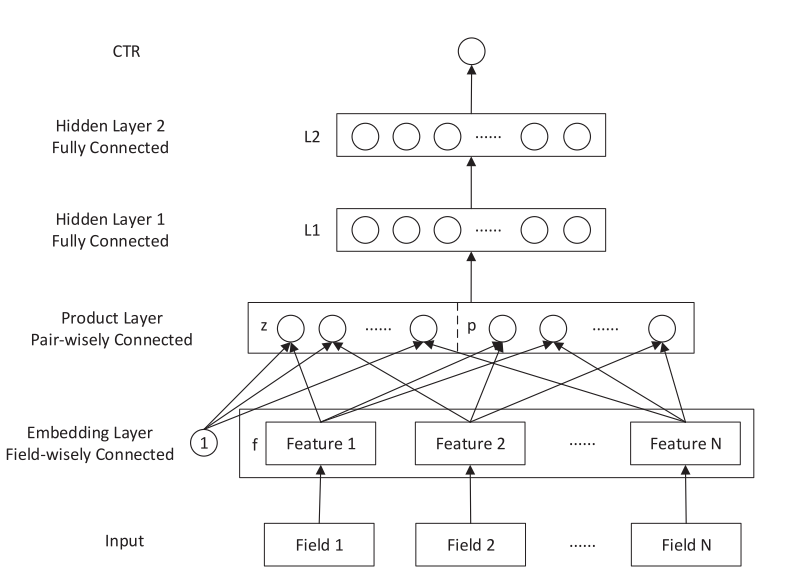
如图中,对于 Product Layer,z 是嵌入后特征和 1 做 Product 的结果,所以就是拷贝了一遍嵌入之后的特征,右边部分的 p 是 field embedding 之后两两做 Product 的结果。
PNN 就是在 Embedding+MLP的结构中添加了一个 Product层,并将 Embedding 的结果与 Product 结果 concat 之后输入 MLP中
根据 Product 的实现不同,PNN 也有多种实现,比如使用向量内积(Inner Product)和外积(Outer Product),对应 IPNN 和 OPNN 。
首先可以看到,两两做 Product 导致至少是输入 field 数目的平方,所以需要对这一部分的计算做优化。
IPNN
Product 使用 Inner Product,这个很简单,有
\[P \in \mathbb{R}^{N \times N}, P_{ij} = f_i^T f_j \in \mathbb{R}\]其中 $N$ 是输入 field 的个数,$f_i \in R^{k}$ 是第 i 个 field Embedding 之后的向量(Embedding 之后维度为 k ) 。记 MLP 第一层的参数为 $W$, 则对应输出为
\[y = \sum_{i=1}^{N} \sum_{j=1}^{N} W_{ij} P_{ij}\]这里 $W, P$ 都是对称矩阵,可以使用一阶矩阵分解来近似 $W$ ,从而降低复杂度(这里跟 FM 中的思想差不多?等看完代码再来深刻理解)。
https://zhuanlan.zhihu.com/p/56651241
OPNN
Product 使用 Outter Product, 有
\[P_{i,j} = f_i f_j^{T} \in \mathbb{R}^{k \times k}\]这个复杂度比 IPNN 更高,作者使用 sum pooling ,即:
\[P = \sum_{i=1}^{N}\sum_{j=1}^{N} P_{ij} = \sum_{i=1}^{N} \sum_{j=1}^{N} f_i f_j^{T} = \left(\sum_{i=1}^{N} f_i \right) \left(\sum_{j=1}^{N} f_j \right)^{T}\]降低复杂度的具体策略与具体的 Product 函数选择有关,IPNN 其实通过矩阵分解,“跳过”了显示的Product 层,通过代数转换直接从 embedding 层一步到位到 MLP 第一层(这不就和 FM 一样了?),而 OPNN 则是直接在 Product 层入手进行优化。
Wide & Deep
结合 LR + DNN。框架图如下
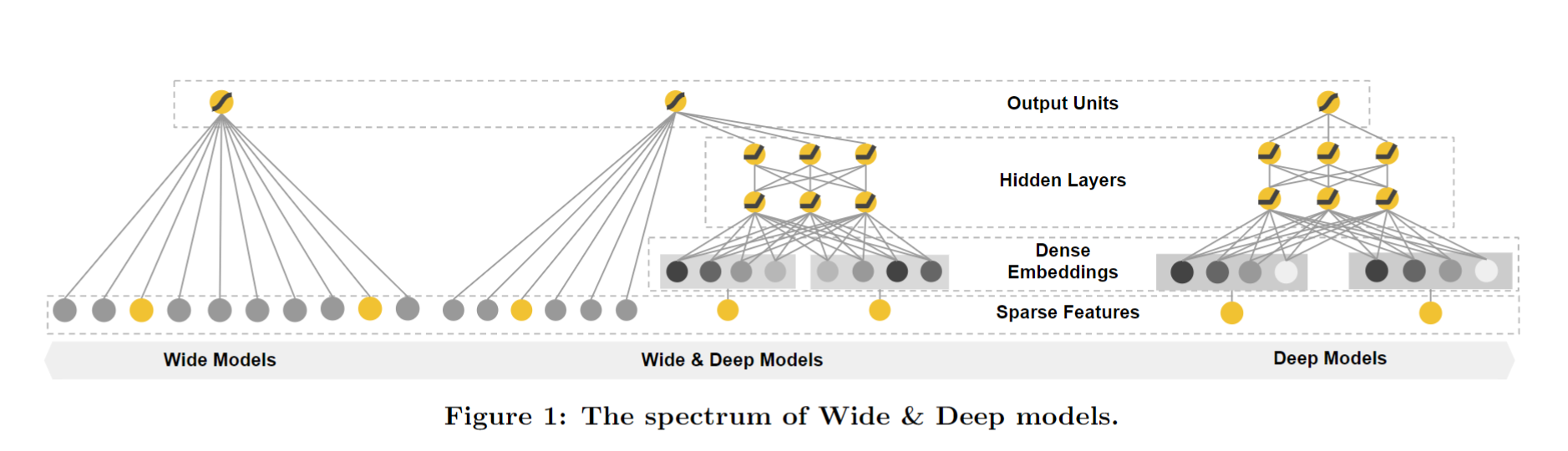
Wide 部分是广义线性模型,即:
\[y = w^t [x, \phi(x)] + b\]其中,x 是原始特征,$\phi(x)$ 是叉积特征。
Deep 部分是前馈神经网络,网络对一些 Sparse Features 进行一个 Embedding(维度通常降到O(10)~O(100)), 然后和一些原始的特征 contcat ,作为网络下一层的输入。
对于隐藏层
\[z = f(W x + b)\]其中 $z$ 是一层的输出, $W, b$ 是隐层参数,$f$ 是激活函数。
Loss function 是 logistic loss。这样最后的输出是
\[p(y=1|x) = \sigma(w^T_{wide}[x, \phi(x)] + w^T_{deep}a + b)\]其中 a 表示最后一层激活值。
如果不对嵌入层预先训练,Wide&Deep 和 Deep Cross 性能比 FM 还差,而且 Deep Cross 严重过拟合,Wide&Deep遇到了degradation问题。如果使用FM预训练初始化嵌入层,Wide&Deep和DeepCross性能都提升了,甚至超过了FM。Wide&Deep的degradation问题也解决了,因为训练集的性能得到了提升。但是两者依旧都有过拟合的问题。
DeepFM
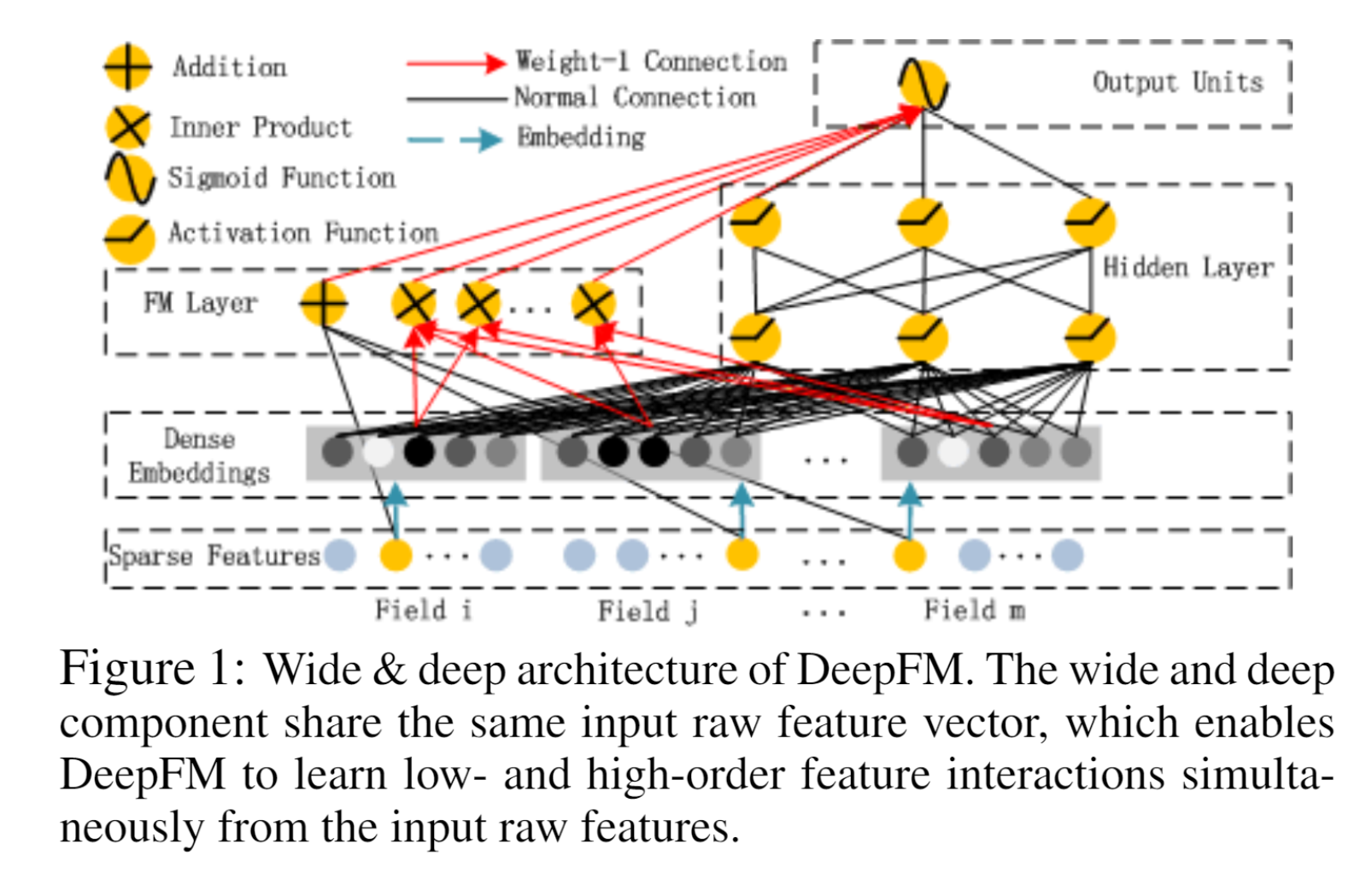
FM + DNN ,借助 FNN 的思想,利用 FM 进行 Embedding ,之后的 wide 和 deep 模型共享 embedding 之后的结果。
Embeddiings
嵌入层首先将稀疏的特征输入压缩为低维稠密向量,如图中 Dense Embeddings 部分。注意
- field 长度不一致,但是都压缩为 k 维向量(latent vector)
- FM 里的隐含变量 V 作为了嵌入层的权重,FM 作为整个模型的一部分一起学习,实现了 end2end
FM 与深度部分共享 embedding 带来的好处是:
- 从原始数据中同时学到了低阶和高阶特征
- 不再需要手动特征工程,(Wide&Deep需要)
这里 Embedding 类似于 word2vec 的过程。特征中有很多都是类别(Categorical)型,进行 one-hot 编码后会非常稀疏。所以我们使用 embedding 将其压缩到低维空间中,成为稠密向量。Embedding 就是一层全连接(参考 word2vec )。
torch 中的实现
# 假如 Sparse_feature 有 500 个不同得取值
sparse_feature = torch.LongTensor([[2]])
# 将 500 维 one-hot 压缩到 32 维
embedding = torch.nn.Embedding(500, 32)
output = embedding(sparse_feature) # output.shape=(batch_size, 1, 32)
keras 中的实现
sparse_feature = np.array([[2]], dtype=np.long) # (batch_size, 1)
embedding = tf.keras.layers.Embedding(input_dim=500, output_dim=32, mask_zero=True)
output = embedding(sparse_feature) # output.shape=(batch_size, 1, 32)
这个过程就是给定一个矩阵 shape=(500, 32), 然后依照给定的值作为 row index 在矩阵找出对应的行(embedding_lookup),这个过程和 one-hot 向量乘与矩阵是一样的。
FM 部分
分别计算线性项和下列二次项
\[\frac{1}{2} \sum_{f=1}^{k} \left[ \left( \sum_{i=1}^{n} v_{i,f} x_i \right)^2 - \sum_{i=1}^{n} v_{i,f}^2 x_i^2 \right]\]DNN 部分
嵌入层的输出为 $a^{(0)} = [e_1, e_2, …, e_m]$ ,其中 $e_i$ 是嵌入的第 i 个 field,m 是 field 的个数,前向过程中:
\[a^{(l+1)} = \sigma(W^{(l)} a^{(l)} + b^{(l)})\]其中 $l$ 是层数,$\sigma$ 是激活函数,$W^{(l)}, b^{(l)}$ 是第 $l$ 层的参数。
DCN
Deep & Cross Network
引入 Cross 取代 wide & deep 中的 wide(从名字就看出来了)。Cross 是一层特殊网络,能够自动地构造有限高阶的交叉特征,并学习对应的权重。
Wide & Deep 里面 Wide 部分仍然需要手动特征工程,费时费力。DCN 的 Motivation 就是尝试自动学习高阶特征组合(所有DNN相关的工作都在这么干)。
网络结构图如下
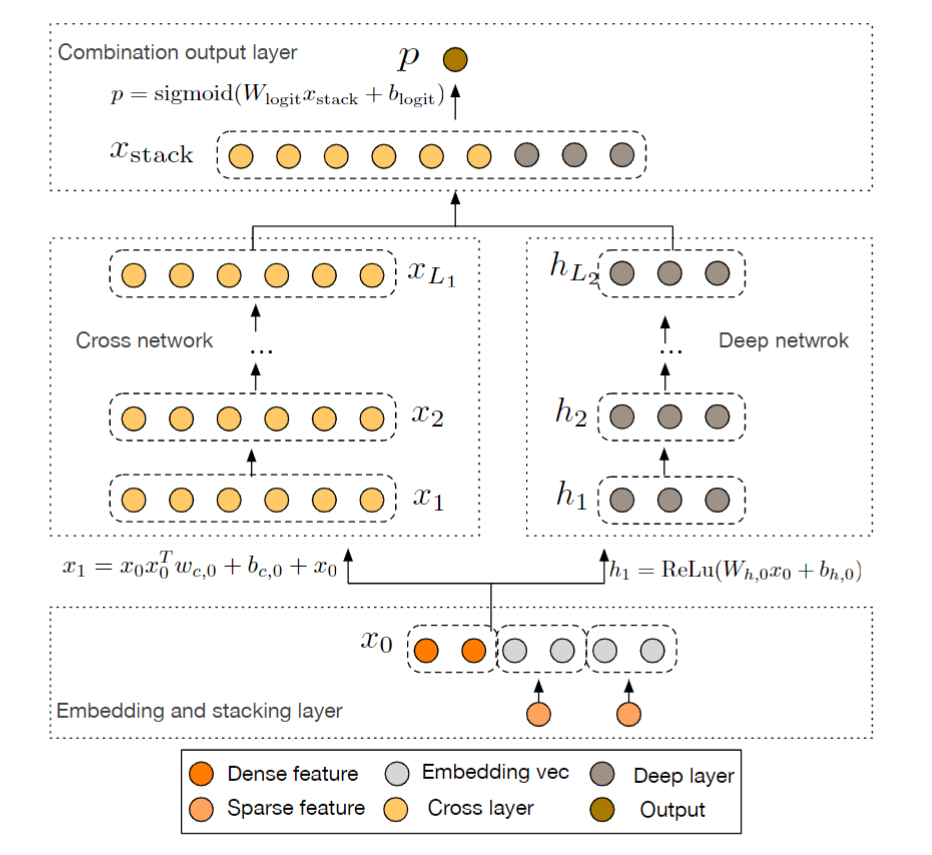
对于特征的处理
- sparse -> embedding
- multi-hot sparse -> embedding + average pooling
- dense -> normalization,之后与 sparse feature concat
Cross
Cross 的目的是显式,自动地构造有限高阶交叉特征,结构如图。

上述结构对应的结算式子为
\[y = x_0 {x}^T w + b + x = f(x;w, b) + x\]显然:
- 每个 Cross 层的神经元个数都相同,都是 $x_0$ 的维度 $d$
- 这里的结构是个残差网络(Residual Network)的残差块(残差是相对与误差而言的,误差指观测值与真实值之间的偏离,残差是观测值与拟合值的偏离, 残差块是 $y=f(x) + x$, y 是预测值,x 是观测值,f(x)对应着残差)
根据 Cross 的计算式子:
- 有限高阶:叉积的阶数由 Cross 的层数决定(最高阶数是层数+1,把 y 代入到下一层公式就看出来了)
- 自动叉积:Cross 最后的输出包含了原始特征从一阶到层数 +1 阶的所有叉积组合,同时保证了模型参数线性增长。
- 参数共享:每个叉积项的权重是多层网络的参数乘积得到的,有效降低了参数量,同时参数共享使得模型有更强的泛化性和鲁棒性
Deep 部分和 Wide & Deep 中一样,就是简单的的全连接。
输出模块 concat Cross 和 Deep 的输出,然后使用 Logistic loss 作为损失函数,整个网络一起训练,另外也加了 L2 正则防止过拟合。
xDeepFM
xDeepFM(eXtreme Deep Factorization Machine) 是将 DeepFM 的二次项部分(FM Quadratic Layer 部分)换成了 CIN。但 xDeepFM 是 DCN 的改进,主要解决 DCN 的如下问题。
DCN 中,Embedding 之后的向量是 concat 的,然后进入 Cross 计算高阶特征时是一个所有特征嵌入后拼接起来的巨大向量,即失去了 Field Vector 的概念,FFM 中是以 Field Vector 为基本粒度的。
这里为什么不是 vector-wise 就不好了?对 FM 理解不够深,需要再深入理解一下 FM 和 FFM ?
CIN
CIN(Compressed Interaction Network) 是一个堆叠型网络,首先 CIN 的输入来自 Embedding 层,假设有 $m$ 个 field ,每个 field 进行 Embedding 之后的维度为 $k$ ,则输入为矩阵 $X \in \mathbb{R}^{m \times k}$
对于每一层,用 $X^l \in \mathbb{R}^{H_l \times k}$ 表示第 $l$ 层的输出, 其中 $H_l$ 是第 $l$ 层 向量的个数,每个向量的维度始终为 $k$ ,具体第 $l$ 层第 $h$ 个向量计算方法为:
\[X_h^l = \sum_{i=1}^{H_{l-1}}\sum_{j=1}^{m} W_{ij}^{l,h} (X_{i}^{l-1} \odot X_{j}^{0}) \in \mathbb{R}^{1 \times k}\]其中, $1 \le h \le H_l$ ,$\odot$ 表示 Hadamard 积。根据上述公式可以看出,每一具体的作用为:
- 取前一层输出 $X^{l-1} \in \mathbb{R}^{H_{l-1} \times k}$ 中的 $H_{l-1}$ 个向量分别于初始输入 $X^0 \in \mathbb{R}^{m \times k}$ 中的 $m$ 个向量两两做 Hadamard 积,得到 $H_{l-1} * m$ 个向量,然后进行加权求和。
- 不同层之间的区别在于,权重矩阵 $W^l \in \mathbb{R}^{H_{l-1} \times m}$
显然与 Cross 差不多都是自动的对 Embedding 之后的向量做叉积,而且同样具有有限高阶,参数共享的性质。不同点在于:
- CIN 想要主要解决的问题 -> vector-wise
- Cross 每一层输出一阶到层数 +1 阶叉积项,CIN 每层只输出层数 +1 阶叉积项
sum pooling 为什么合理?如果 CIN 层数为 1 ,且 $H_1 = m$ ,权重矩阵恒为 1 ,那么 sum pooling 的结果就是两两向量之积(对应 FM 的 Quadratic Layer)
xDeepFM 极其容易过拟合(这要看不同的任务场景)。所以可以尝试一下特征的离散化,以及对cin和dnn都适当的加上 dropout。
DIN
[排序] [2017,alimama] 普通的加入 DNN 的方法,直接把用户行为的历史数据进行建模,然而在比如电商利用,用户是否会点击一个推荐的商品,并不依赖于所有的历史行为,而是依赖部分历史行为;另外还需考虑多样性。
DIN 就是同时对 Diversity 和 Local Activation 进行建模。
- 对于 Diversity, 即用户广泛的兴趣,DIN 使用 An interest distribution 表示。
- 对于 Local Activation,使用了 Attention 机制,具体就是模型在预测时对不同历史行为关注程度是不一样的。
- 当 DNN 参数多时,输入又很稀疏时,很容易过拟合,DIN 使用 Adaptive regularization 来防止。
特征处理 >Learning piece-wise linear models from large scale data for ad click prediction< 参考里面的 common feature trick,目的是降低空间和计算开销。 大体思想为:同一个用户多条样本,他们之间有很多信息重复,比如用户统计信息,昨天之前的统计信息等。针对这些重复信息只存储一次,并建立索引。
另外,把特征分为四类:用户特征,用户行为特征,广告特征,上下文特征,没有进行特征交叉,而是使用过 DNN 学习特征交互信息。
另外只有用户行为特征中有 multi-hot,这导致了每个用户样本长度不同,我们使用
Embedding -> Pooling + Attention
来解决这个问题。
评价指标 使用的时 GAUC
AUC 表示正样本得分比负样本得分高的概率。CTR 常用来预测对每个用户候选广告的排序,但是不同用户存在差异:有些人天生点击率高,GAUC 使用了展示次数/点击次数进行加权平均的 AUC 。
\[GAUC = \frac{\sum_{i=1}^{n} w_i * AUC_i}{\sum_{i=1}^{n} w_i}\]其中 $w_i$ 可以取 impression 或者 clicks, $n$ 是用户数量。
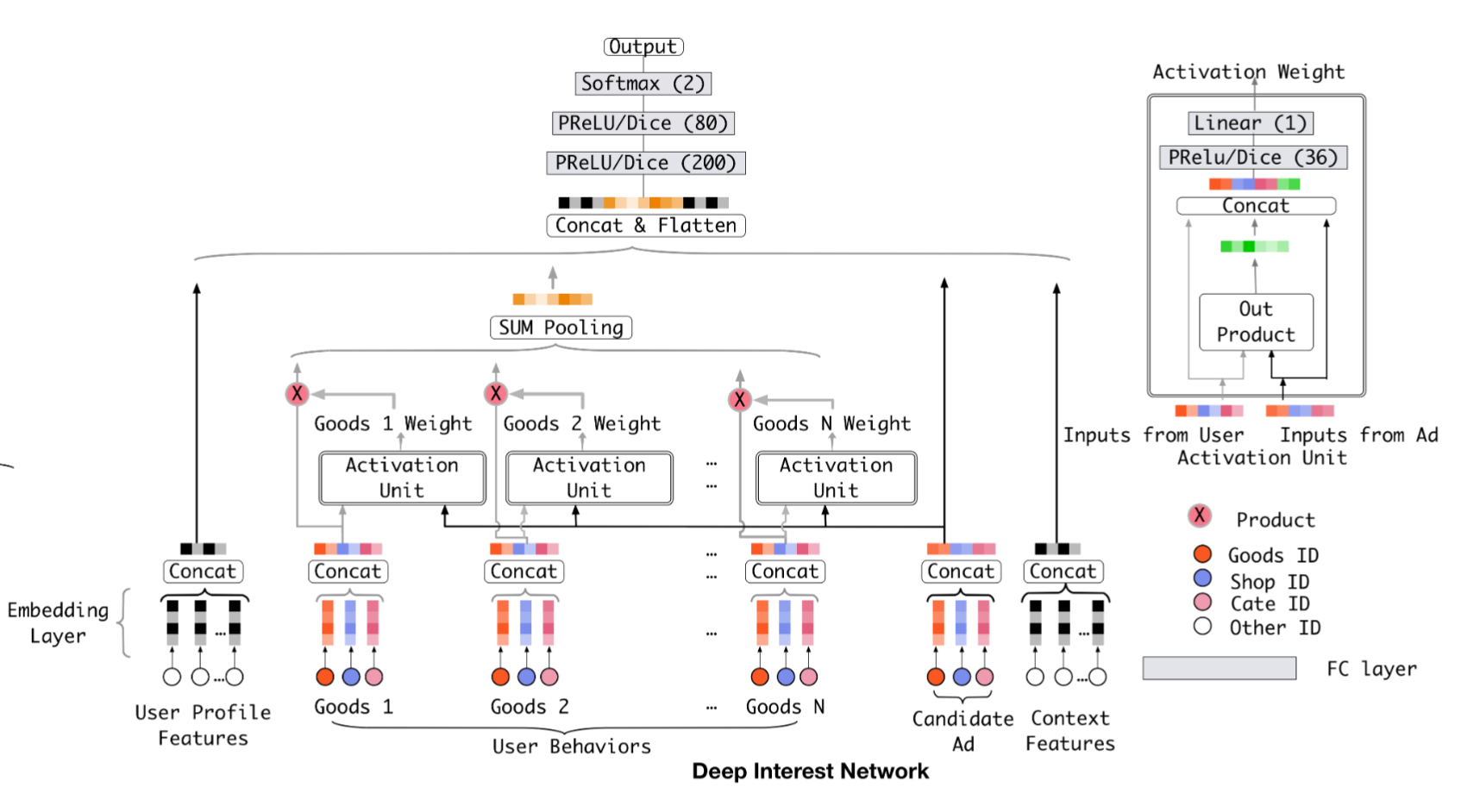
上图中,对于用户特征,上下文特征直接 Embedding + concat 输入到 DNN 中,而对于候选广告特征除了 Embedding + concat 之外,还和用户行为特征在 Embedding 空间中学习一组权重(即Attetion),之后使用 Sum Pooling 后再其他几种特征 concat 一起输出 DNN,Sum Pooling 实现对 Diversity 建模。。
Activation Unit 就是用于实现 Attention 机制的部分,用于对 Local Activation 建模,网络的结构也很简单,注意里面的激活函数使用的是 PReLU/Dice。
用户历史行为和候选广告,都会被映射到 Embedding 空间,所以在 Embedding 空间中学习二者的关系。同时用户的兴趣点可能会大于 Embedding 的向量维度,因此,DIN 将用户兴趣建模为多峰分布,这样,即使映射到了低维空间,嵌入向量也具有很强的表达能力。记用户兴趣的 Embedding Vector 为 $V_u$,候选广告是 $V_a$,则 $V_u$ 是关于 $V_a$ 的函数,即,用户针对不同的广告有着不同的兴趣表示:
\[V_u = f(V_a) = \sum_{i=1}^N w_i \cdot V_i = \sum_{i=1}^N g(V_i, V_a) \cdot V_i\]其中,$V_i$ 表示行为 $id_i$ 的嵌入向量,$V_u$ 表示所用行为 ID 嵌入向量的加权和,表示用户兴趣,候选广告影响着每个行为 ID 权重,在实际中,权重通过 PReLU/Dice 激活函数来输出,$g(V_i, V_a)$ 对应一个 Activation Unit。
Dice PReLU 是带参数的,在 x < 0 时学习一个参数来避免 Dead ReLU 的问题,但它的突变点依然是在零点。而 DIN 认为突变点应该是依赖于数据的,这就是 Dice 激活函数。
\[\begin{aligned} f(x) &= \alpha (1-p(x)) \cdot x + p(x) \cdot x \\ p(x) &= \frac{1}{1 + e^{-\frac{x-E[x]}{\sqrt{Var(x) + \epsilon}}}} \end{aligned}\]其中,$E[x]$ 和 $Var(x)$ 分别是 mini-batch 内的均值和方差,在 testing 阶段,使用的所有数据的 Moving Average. $\epsilon$ 是一个小常数,例如 1e-8。可以看出,$p(x)$ 是一个概率(经过均值归一化,然后输入一个 sigmoid 函数),同时起到整流的作用,决定 $f(x)$。
Adaptive Regularization 解决过拟合 DNN 模型复杂,参数多,而输入稀疏,所以很容易过拟合。已有的 L1, L2, Dropout 防止过拟合的方法,DIN 中试验过后效果并不好。
对于 CTR 中的数据,很多 feature id 就只出现过几次,然后小部分 feature id 出现很多次(长尾理论)这在训练中带来了很多噪声,并且加重了过拟合。
简单粗暴的办法:设置阈值过滤,缺点是阈值选定依赖经验,并且丢失的信息无法评估。
DIN 给出的解决办法:针对 feature id 出现的频率,自适应正则化强度。
- 出现频率高的,使用较小的正则化强度
- 出现频率低的,使用较大的正则化强度(防止过度拟合出现次数少的数据)
其中 $B$ 是 mini-batch 的样本,大小为 $b$,$n_i$ 是出现频率,$I_i$ 表示我们考虑特征非零的样本。
Youtube DNN
[召回]+[排序] 两个 NN,一个用来召回,一个用来 ranking。 Youtube 中面对的 3 大调整:
- Scale : 规模庞大
- Freshness: 新鲜的,新旧视频的推荐
- Noise: 噪音,数据稀疏,隐私反馈,存在大量噪声
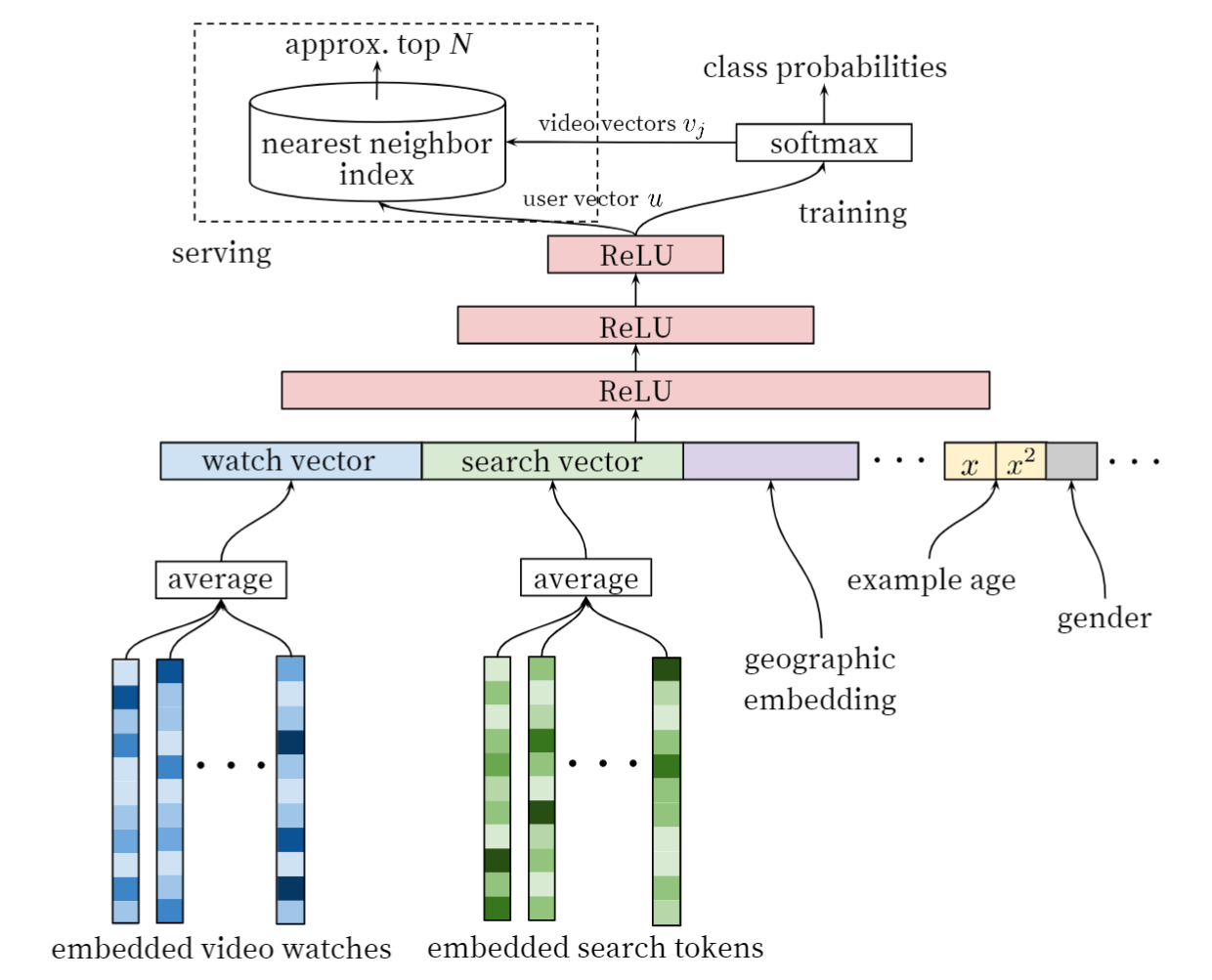
Youtube 将推荐问题看成一个超大规模多分类问题,即某一用户 $U$ 在上下文 $C$,时刻 $t$ 观看一个视频的概率:
\[P(w_t = i|U, C) = \frac{e^{v_iu}}{\sum_{j \in V} e_j u}\]其中 $u \in \mathcal{R}^N$ 是用户历史行为和上下文的嵌入向量(用户兴趣向量),$v_j \in \mathcal{R}^N$ 表示每个视频的嵌入向量。
因此整体目标就是在给定用户历史行为和上下文的情况下,学习出用户的嵌入向量 $u$,接着使用 softmax 分类器来召回视频。由于视频的数目巨大,计算 softmax 需要遍历语料库中的所有视频,计算量巨大,关键问题就是高效训练。
MIND
[召回] 召回阶段的处理用户多样化兴趣的算法。
目前召回的主流算法是协同过滤和向量化召回,协同过滤面临稀疏性问题,而向量化方法比如 youtube DNN, 将用户的兴趣表示成一个固定长度的向量。
而本文的核心思想主要又两个:
- 单个用户采用多个向量表示其行为特征(label-aware attention)
- 使用动态路由机制来挖掘用户的多层次兴趣。
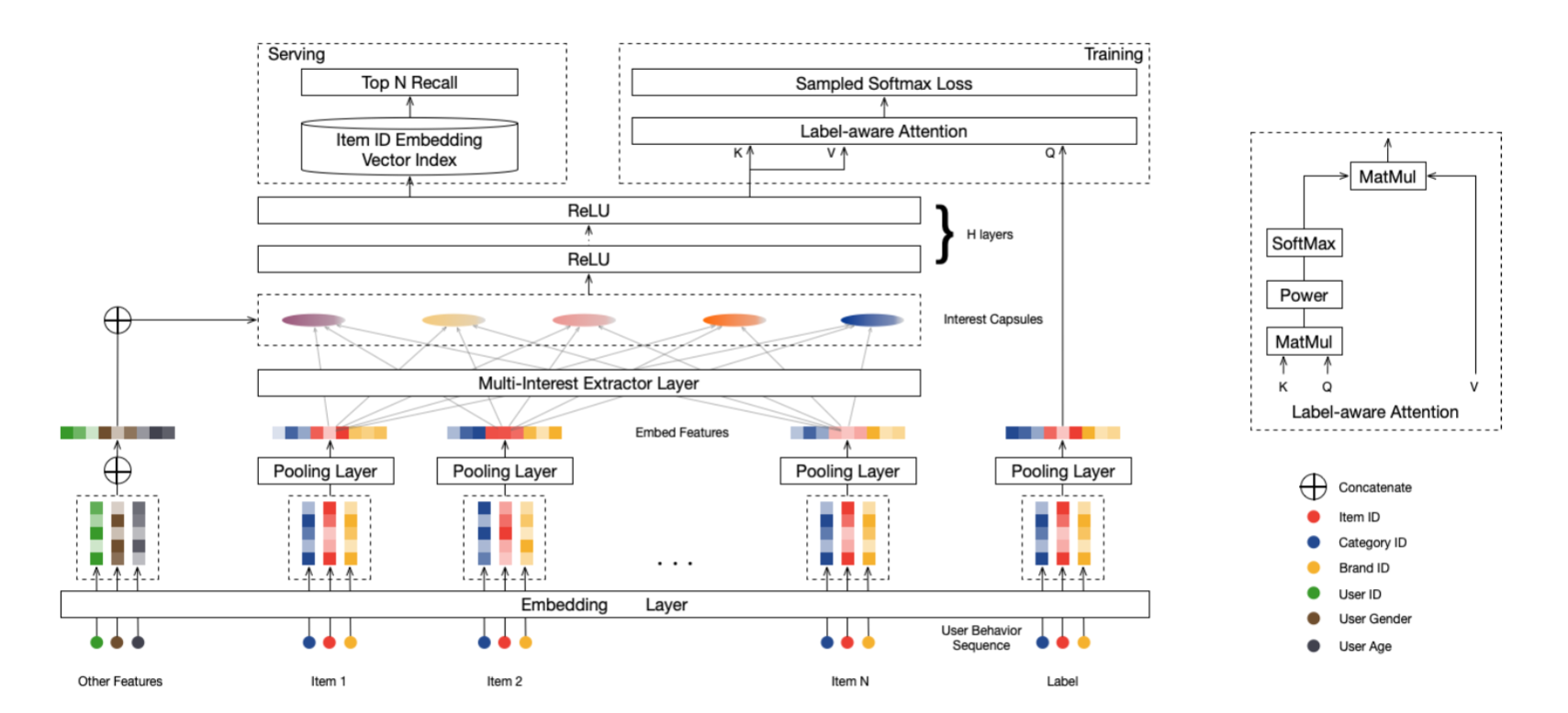
召回的任务是为每个用户 $u \in \mathcal{U}$ 从商品集合 $\mathcal{I}$ 选取个很小的商品子集。为此需要用到以下三部分数据:
- $\mathcal{I}_u$ 用户历史行为特征
- $\mathcal{P}_u$ 用户特征
- $\mathcal{F}_i$ 目标商品特征(商品 ID,类别 ID)
MIND 的核心任务是学习用户行为特征的多个表征向量的映射
\[V_u = f_{user}(\mathcal{I}_u, \mathcal{P}_u)\]其中 $V_u = (\vec{v}_u^1, …, \vec{v}_u^K) \in \mathbb{R}^{d \times K}$,其中 $d$ 是向量维度,$K$ 是表征向量的个数,当 $K = 1$ 时,就是只有一个嵌入向量,这时就是 YouTube DNN。
另外,目标商品 $\mathcal{F}_i$ 的表示向量通过一个嵌入函数获取。
\[e_i = f_{item}(\mathcal{F}_i)\]其中,$e_i \in \mathbb{R}^{d\times 1}$ 用一个向量表征商品信息。
得到了用户和商品的向量表示之后,通过如下的 score 公式获取到 topN 的商品候选集。
\[f_{score} (V_u, e_i) = \underset{1\le k \le K}{\max} e_i^T v_u^k\]Embedding & Pooling Layer
由图上可见,三组输入,$\mathcal{I}_u, \mathcal{P}_u, \mathcal{F}_i$, 首先通过 Embedding 层将属于的稀疏向量嵌入到低维稠密向量中,用户特征的 ID 类(比如性别,年龄)通过了 Embedding 之后进行了 concat, 而目标商品的特征嵌入之后通过了一层 Pooling Layer 形成了最终的嵌入目标商品向量,用户行为特征通过 Embedding 和 Pooling 之后得到了一组行为特征嵌入向量。
Multi-Interest Extractor Layer 这里是本文的关键,因为一个嵌入向量不足以表示用户多样的兴趣,因此学习多个嵌入向量。这里是受到了基于 Hinton 提出的胶囊网络(Capsule输入是一组向量,对这组向量进行仿射变换之后求加权和,把加权和输入非线性激活函数得到一个向量的输出)动态路由方法的启发。这里就暂时记住,在 MIND 中,所有输入向量共享一个仿射矩阵(由于共享仿射矩阵,权重初始化改为随机),同时输入一组向量,输出一组向量。
Label-aware Attention Layer 这里采用了类似 DIN 中的做法,再得到了用户兴趣向量之后,由于不同用户的兴趣向量的个数不同,通过 Label-aware Attention Layer 对这些向量进行加权(只应用训练阶段)。对应网络结构的计算公式为:
\[v_u = Attention(e_i, V_u, V_u) = V_u softmax(pow(V_u^Te_i, p))\]对应图中就是 Q 是目标商品的 Embedding 向量,而 K,V 都是用户的兴趣向量。这里在 softmax 之前对$V_u^Te_i$ 进行了一定的缩放,当 $p$ 接近零时,对 softmax 起平滑作用,当 $p$ 大于 1 时,对 softmax 起 sharpen 作用,此时直接选择 attention score 最大那个兴趣向量(p 超参数)。
Trainning & serving
在训练阶段,使用 Label-aware Attetion Layer 得到用户向量和目标商品的 Embedding,计算用户 $u$ 和商品 $i$ 的交互的概率(和youtube DNN 相似)(softmax 函数) \(Pr(i|u) = Pr(e_i|v_u) = \frac{\exp(v_u^Te_i)}{\sum_{j \in \mathcal{I}}(v_u^Te_j)}\)
目标函数为: \(L = \sum_{(u, i) \in \mathcal{D}} \log Pr(i|u)\)
在 Serving 阶段,只需要计算用户的多个兴趣向量,然后每个兴趣向量通过最近邻算法(如局部敏感哈希)来得到最相似的候选商品集合。同时,当用户产生了一个新的交互行为,MIND 也可以实时响应得到用户新的兴趣向量(实时更新)。
待补充
经典文
ItemCF
[召回] 协同过滤的一种,基于物品的协同过滤。基本思想是给 User 推荐他们喜欢过的物品的相似物品,同时在处理相似性上认为Item A 与 Item B 相似是因为大多喜欢 Item A 的用户也喜欢 Item B。
算法主要分为两个步骤。
- 计算物品之间的相似度
- 根据物品的相似度和用户的历史行为生成推荐列表
物品 $i$ 和 $j$ 之间的相似度
\[w_{i,j} = \frac{|N(i)\cap N(j)|}{\sqrt{|N(i)| |N(j)|}}\]| 其中 $ | N(i) | $ 是喜欢物品 $i$ 的用户数,$ | N(i)\cap N(j) | $ 是同时喜欢物品 $i$ 和物品 $j$ 的用户数(这就对应第二个思想)。然后就可以根据此公式求出相似性矩阵 $W$. |
计算用户 $u$ 对物品 $j$ 的兴趣,给用户生成推荐列表
\[P_{u,j} = \sum_{i\in N(u) \cap S(j, k)} w_{j,i} r_{u,i}\]其中 $P_{u,j}$ 表示用户 $u$ 对物品 $j$ 的兴趣,$N(u)$ 表示用户 $u$ 喜欢的物品集合,$S(j, k)$ 表示和物品 j 最相似的 $k$ 个物品的集合, $W_{j,i}$ 是上面的相似度,R_{u, i} 是用户 $u$ 对物品 $a$ 的兴趣。
对应相似度计算还有考虑了用户的活跃度的改进,认为活跃的用户对物品相似度的贡献少,所以增加一个 IUF (Inverse User Frequence) 参数来修正物品相似度计算公式:
\[w_{i,j} = \frac{\sum_{u \in N(i) \cap N(j)} \frac{1}{\log(1+|N(u)|)}}{\sqrt{|N(i)||N(j)|}}\]
LR + GDBT (Facebook)
[排序] LR 是 CTR 预估中用的最多的模型,但是线性模型加上一个 sigmoid ,线性模型表达能力不足,所以对特征组合很关键,人工特征组合耗时费力还不一定有提升。因此本文是利用 GDBT(Gradient Boost Decision Tree) 解决 LR 的特征组合问题。
GDBT 是一种常用的非线性模型,基于 ensemble 中的 boosting 思想,每次迭代都在减少残差的梯度放下新建立一个决策树,GBDT 的思想使其具有天然优势可以发现多种有区分性的特征以及特征组合(GDBT 也是一种常用来发现特征组合的有效思路),决策树的路径可以直接作为 LR 输入特征使用,省去了人工寻找特征、特征组合的步骤。
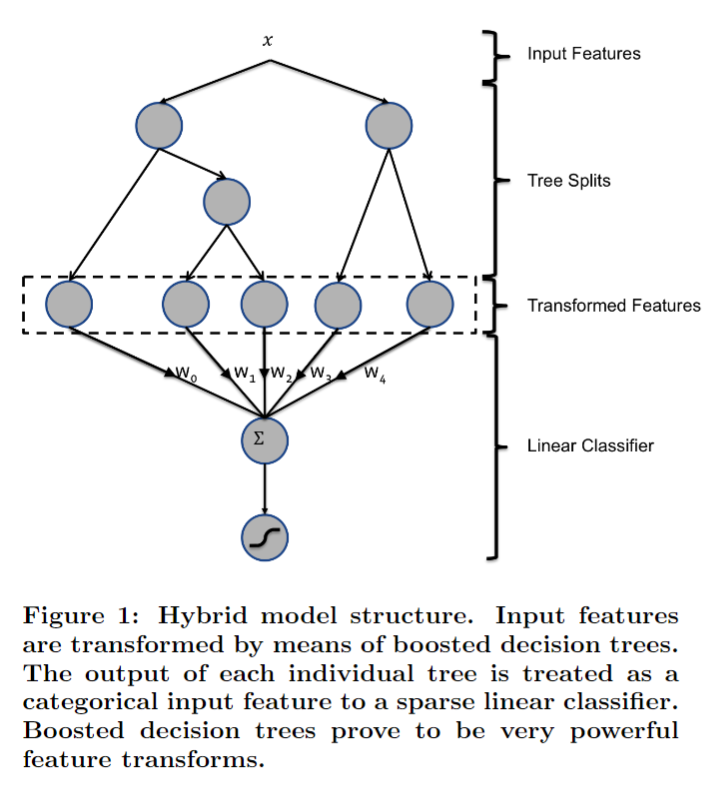
如上图中的一个模型,总共有两棵树,左边树有三个叶子节点,右边树对应有两个个叶子节点(图中 Transformed Features 层),如果一个输入 x 对应到了左边树的第二个叶子节点,则对应特征被编码为 [0,1,0], 如果 x 对应到了右边树的第一个叶子节点,则对应编码为 [1,0], 于是 x 通过 GDBT 后被编码为 [0,1,0,1,0]。
评价指标:Normalized Cross-Entropy(NE)
\[NE = \frac{-\frac{1}{N}\sum_{i=1}^{n}(\frac{1+y_i}{2}\log(p_i) + \frac{1-y_i}{2}\log(1-p_i))}{-p\log(p) - (1-p)\log(1-p)}\]其中,$N$ 为样本数,$y_i$ 是样本标签,$p$ 为平均历史点击率, 分母是 backgroud CTR 使得NE 对 backgroud CTR 不敏感。NE 与相对信息增益(Relative Information Gain, RIG)的关系, $RIG = 1 - NE$
Calibration:
- Calibration 校准是平均预测 CTR 与经验 CTR 的比值,是一个比值。
- Calibration 越接近 1 , 模型性能越好
AUC 非常不错的平价指标,但存在一个问题,当我们模型预测的 CTR 偏高 2 倍时,们可以通过Calibration校准,使用一个全局的0.5的系数来修正。修正之后NE也会提高,而AUC却保持不变。 这一段没看懂。
两个关键点:采用ensemble决策树而非单颗树;建树采用GBDT而非RF(Random Forests
-
为什么建树采用 enssemble 决策树(Why ensemble?)
多棵树的表达能力更强,GDBT 每次迭代都在减小残差的放下上学习一颗新树,迭代多次对应生成多少棵树。同时多棵树,正好满足训练样本通过 GDBT 映射成多个特征。
-
为什么建树采用 GDBT 而不是 RF(random forest)(Why GDBT not RF?)
RF 也是多棵树,但在实践上证明不如 GDBT。且,GDBT 前面的树,特征分裂主要体现对多数样本有区分度的特征;后面的树,主要体现经过前面的树后,残差仍然较大的少数样本。
FTRL(Follow The Regularized Leader)
Google 提出的在线学习算法,工程上应用广泛,大量优化。在线学习可以利用流式的数据(比如大批数据分批读入内存或者来自网络的数据)进行学习,同时推荐系统中项目的特征维度很高,但实际上一个样本的非空维度很少。
FTRL-Proximal 是结合了 FOBOS 的精度和 RDA 的稀疏性,用于提高 CTR 任务的效果。
Online GD 不够稀疏 -> FOBOS 能产生更加好的稀疏特征(梯度下降类方法,精度比较好),稀疏解是机器学习中很看重得东西,尤其是在工程应用中,稀疏解会大大减少 predict 时得内存和复杂度。
RDA -> 可以在精度和稀疏性之间做更好的平衡(稀疏性更加好)
FTRL-Proximal 的更新公式:
\[w_{t+1} = \arg \min_w (\sum_{s=1}^{t} g_s \cdot w + \frac{1}{2} \sum_{s=1}^{t}\sigma_s \|w-w_s\|_2^2 + \lambda_1 \|w\|)\]上述公式当 $\lambda_1=0$ 时,等价于 SGD 的更新过程 $w_{t+1} = w_t - \eta_t g_t$ 。证明如下:
记 $f(w) = \sum_{s=1}^{t} g_s \cdot w + \frac{1}{2} \sum_{s=1}^{t}\sigma_s |w-w_s|_2^2$,则 $f(w)$ 是一个凸函数,求极值在导数等于 0 时取到
\[\frac{\partial f(w)}{\partial w} = \sum_{s=1}^t g_s + \sum_{s=1}^t \sigma_s (w-w_s) = 0\]即:
\[\sum_{s=1}^t \sigma_s w_{t+1} = \sum_{s=1}^t(\sigma_s w_s - g_s)\]因为 $\sigma_s$ 定义为: $\sum_{s=1}^t\sigma_s = \frac{1}{\eta_t}$,则上面式子化为:
\[\frac{1}{\eta_1} w_{t+1} = \sum_{s=1}^t \sigma_s w_s - \sum_{s=1}^t g_s\]使用错位相减法,用 $t-1$ 替换上式 $t$,并联立两式如下
\[\left\{ \begin{aligned} \frac{1}{\eta_t} w_{t+1} &= \sum_{s=1}^t \sigma_s w_s - \sum_{s=1}^t g_s \\ \frac{1}{\eta_{t-1}} w_{t} &= \sum_{s=1}^{t-1} \sigma_s w_s - \sum_{s=1}^{t-1} g_s \end{aligned} \right.\]两式相减得:
\[\frac{1}{\eta_t} w_{t+1} - \frac{1}{\eta_{t-1}} w_t = \sigma_t w_t - g_t = (\frac{1}{\eta_t} - \frac{1}{\eta_{t-1}}) w_t - g_t\]化简:
\[\frac{1}{\eta_t} w_{t+1} = \frac{1}{\eta_t} w_t - g_t\]同时乘上 $\eta_t$ 得:$w_{t+1} = w_t - \eta_t g_t$ 。
实际使用中,还会加上 L2 正则,这样 FTRL 更新策略为
\[w_{t+1} = \arg\min_w (g_{1:t}\cdot w + \frac{1}{2}\sum_{s=1}^{t} \sigma_s \|w-w_s \|^2 + \lambda_1 \|w\| + \frac{1}{2}\lambda_2 \|w\|^2)\]其中 $g_{1:t} = \sum_{s=1}^{t} g_t$ ,相当于新产生的权重验证所有样本的梯度并和历史权重不偏离太远。最后通过 L1 正则进行稀疏性约束。这样即保证了权重的更新的精度又保证了稀疏性。
另外,参数 $\sigma_s$ 是一个和学习率相关的参数 $\sum_{s=1}^{t} \sigma_s = \frac{1}{\eta_t}$,而 $\eta_t = \frac{1}{\sqrt{t}}$ 非递增序列。
算法如下:

其中更新过程的推导:依然记
\[\begin{aligned} f(w) &= g_{1:t}\cdot w + \frac{1}{2}\sum_{s=1}^{t} \sigma_s \|w-w_s \|^2 + \lambda_1 \|w\| + \frac{1}{2}\lambda_2 \|w\|^2 \\ &= g_{1:t}\cdot w + \frac{1}{2}\sum_{s=1}^{t} \sigma_s (w^Tw -2w^Tw_s + w_s^Tw_s) + \lambda_1 \|w\| + \frac{1}{2}\lambda_2 \|w\|^2 \\ &= (g_{1:t} - \sum_{s=1}^{t} \sigma_s w_s) w + \frac{1}{2}(\sum_{s=1}^{t} \sigma_s +\lambda_2) w^Tw \lambda_1 \|w\| + Const \\ &= z_t^T w + \frac{1}{2} (\frac{1}{\eta_t} + \lambda_2) w^T w + \lambda_1 \|w\| + Const \end{aligned}\]其中 $z_t^T = g_{1:t} - \sum_{s=1}^{t} \sigma_s w_s$,于是有
\[z_{t-1} = g_{1:t-1} - (\sum_{s=1}^{t-1} \sigma_s w_s )\]所以:$z_t = z_{t-1} + g_t - (\frac{1}{\eta_t} - \frac{1}{\eta_{t-1}}) w_t$
对 $f(w)$ 求导可得:
\[\frac{\partial f(w)}{\partial w} = z_t + (\frac{1}{\eta_t} + \lambda_2) w + \lambda_1 \frac{\partial (|w|)}{\partial w} = 0\]从上式可知,$w$ 和 $z$ 必然是异号,否则等式不成立,根据 L1 的偏导数公式,讨论如下。
\[\frac{\partial (|w|)}{\partial w} = \left \{ \begin{aligned} &0 \quad; \text{if -1 < $w$ < 1} \\ &1 \quad; \text{if w > 1}\\ &-1 \quad; \text{if w < -1} \end{aligned} \right.\]- 当 $|z_{i}| < \lambda_1$ 时 $w_i > 0$,则有 $w = \frac{-z_i-\lambda_1}{\frac{1}{\eta_t} + \lambda_2} < 0$ 不成立; $w_i < 0$,则有 $w = \frac{-z_i+\lambda_1}{\frac{1}{\eta_t} + \lambda_2} > 0$ 不成立; $w_i = 0$;
- 当 $z_i > \lambda_1$ 时 由于两者必须异号,因此 $w_i < 0$, 此时 $w = \frac{-z_i+\lambda_1}{\frac{1}{\eta_t} + \lambda_2}$
- 当 $z_i < - \lambda_1$ 时,同上有 $w = \frac{-z_i-\lambda_1}{\frac{1}{\eta_t} + \lambda_2}$
综上
\[w_i = \left \{ \begin{aligned} &0 \quad &; \text{if }|z_{i}| < \lambda_1 \\ &\frac{-(z_i- sign(z_i)\lambda_1)}{\frac{1}{\eta_t} + \lambda_2} \quad &; \text{otherwise} \end{aligned} \right.\]工程优化
- 各个维度使用不同的学习率$\eta_t = \frac{\alpha}{\beta + \sqrt{\sum_{s=1}^t g_{s_i}^2}}$;
- 稀疏特征处理的办法:泊松分布(使用一定概率丢掉特征),Bloom 过滤器(通过碰撞优化特征);
- 浮点数重新编码(w 的数值分布区间小,省内存);
- 多个模型,不同参数;
- 学习率更新优化通过$\sum g_{1:t}^2 = \frac{PN}{P+N}$ 通过正负样本个数优化;