算法总结-排序
最近一口气肝了400多道Leetcode(肝到做梦都是在刷题),有些题目感觉有点囫囵吞枣,并没有很好的消化吸收,意识到这样疯狂的刷题并不好,应该认真总结,毕竟题是肝不完的,应该做到举一反三,重点是学会思想和灵活运用。
恰好之前我哥说想入门一下IT行业,我给他总结了大概的思维导图,也乘这个机会梳理一下自己的知识体系。之后也会把机器学习的笔记整理一下,总之内容应该非常多,而且杂,也不知道自己啥时候能够整理完,慢慢坚持吧(先给自己立个flag)。
bool flag = true; //这是一个flag
首先放一下思维导图,这个系列只总结CS相关知识,目前的思维导图只是第一版,以后想到了可能会有修改或者补充。
编程语言这一部分就直接跳过,重点梳理数据结构和算法,代码示例以python为主,会穿插一些C++,主要是为了巩固一下STL的掌握。
这一篇就从最基本的算法开始,排序。
排序算法常用的有冒泡,插入,选择,堆排序,快排,归并。其他的还有希尔,计数,桶,和基数。其中桶和基数排序不是基于比较的。
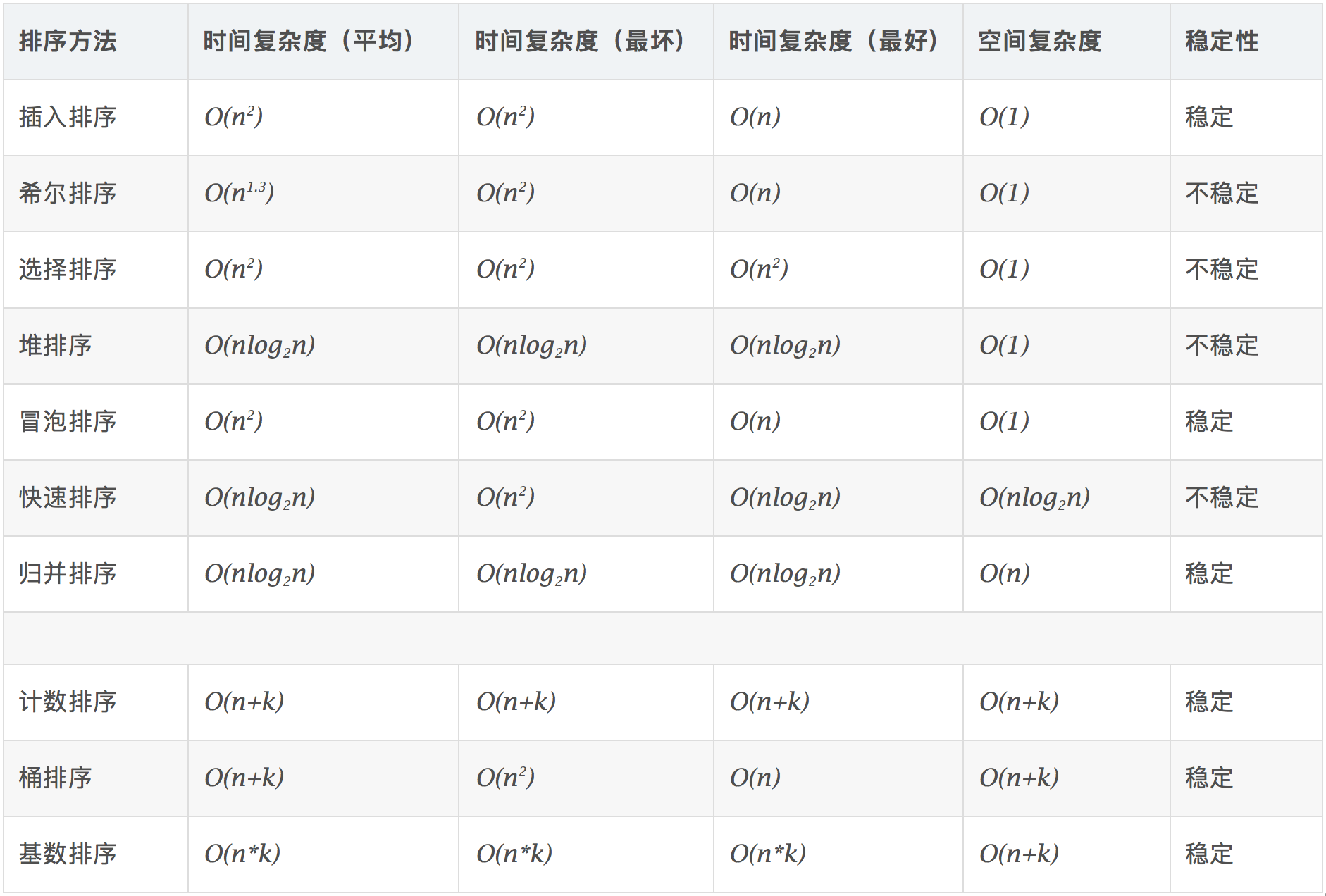
排序基本上在线性表上进行,顺序表的排序比较简单,日常使用也不会真的写,大家都是调包侠。python3中使用list.sort()或者sorted()函数来实现排序,默认使用升序排列,关键字参数key提供比较的方法,cmp函数要使用functools中的cmp_to_key转换为key的实参;关键字reverse默认为False,设置为True是降序排列, 这个排序是稳定的。
ls = [3,4,2,1,5]
ls.sort() # in-place, 返回None
tmp = sorted(ls) # ls保持不变,返回排序的list给tmp
C++使用STL中algorithm头文件中的sort函数,参数是容器的排序元素起止位置的迭代器或者是数组元素的指针,同样可以提供cmp函数,但要注意C++执行严格弱序,因此cmp中只能写return a<b;而不能写成return a<=b;C++的等于要通过 !(a<b) && !(b<a)来推断。这个sort是不稳定的,稳定要用stable_sort()函数。
#include <iostream>
#include <algorithm>
#include <vector>
int main(){
vector<int> vec{3,4,2,1,5};
sort(vec.begin(), vec.end());
return 0;
}
比较有趣的是单链表的排序,单链表由于只能从头顺序向后访问,所以上述的许多算法都不适合(转换成数组再排序的不在考虑之列)。单链表排序有两种方法,一种是交换节点值,另外一种是移动节点。这里主要记一下移动节点方式的链表快排/归并排序。对应LeetCode148题,其中元素划分部分类似于LeetCode86。
class Solution_148:
def _sortList(self, head: ListNode) -> ListNode:
def quick_sort(head):
if not head or not head.next:
return head
p = pivot = head
smaller = ListNode(None)
greater = ListNode(None)
stail = smaller
gtail = greater
t = head.next
while t:
if t.val < pivot.val:
stail.next = t
stail = stail.next
elif t.val == pivot.val:
p.next = t
p = p.next
else:
gtail.next = t
gtail = gtail.next
t = t.next
stail.next = None
gtail.next = None
p.next = None
smaller.next = quick_sort(smaller.next)
greater.next = quick_sort(greater.next)
if smaller.next:
t = smaller.next
while t.next:
t = t.next
t.next = pivot
p.next = greater.next
return smaller.next
else:
p.next = greater.next
return pivot
return quick_sort(head)
这个题目的关键在于链表的操作中不能断链,所以要保证断开和重新链接的正确,归并排序的比较简单,思想用到了LeetCode21题,合并两个有序的链表,只要同样的将链表划分,然后最小的时候一定有序,之后再归并两个有序链表就行了。之后就扩展到了LeetCode23-Merge k sorted Lists,这里应该使用堆结构来获取k个中最小的,之后再说吧,同时如果k个sorted lists是均衡的话,也可以使用败者树结构,它有着比堆更少的比较次数。
排序作为基础操作在算法题中很少单独考察, 大多数时候对数据预先排序处理,可以降低算法的复杂度。比如LeetCode15. 3 Sum。这是一道经典的双指针(Two pointer)题,如果直接暴力枚举,时间复杂度将是O(n^3) 。首先使用排序,再使用指向大的和指向小的两个指针来进行搜索,可以将复杂度降到O(n^2)。算法如下,同时算法中使用了set来去重。
class Solution_15:
def threeSum(self, nums):
# two pointers, 排序后搜索,O(n^2)
res = set()
nums.sort()
for i in range(len(nums) - 2):
j = i + 1
k = len(nums) - 1
a = nums[i]
while j<k:
b, c = nums[j], nums[k]
if a + b + c > 0:
k -= 1
elif a + b + c == 0:
res.add((a, b, c))
while j<k and nums[j] == nums[j+1]: j+=1
while j<k and nums[k] == nums[k-1]: k-=1
k -= 1
else:
j += 1
return list(res)
今儿就写这么多吧~